Sail by Night Physics
Machine learning, applying it requires very little knowledge, but understanding it can be frighteningly difficult.This often gives a misleading sense of making progress, while it can make people unable to see that they’re still walking at the same place. I’ve always believed that machine learning can indeed offer breakthroughs, but I also believe it’s not that simple.
One should first study physics properly, truly understand what problem is being solved. If you just stare at the loss function all day to see if it is decreasing, it will be easy to forget that your original goal was to study nature.
Reproducing results in ML-for-PDE-solving research using stronger baselines, by Nick McGreivy in
"I got fooled by AI-for-science hype — here's what it taught me"
| Article | Number of citations | Partial Differential Equation | Weaker baseline | Stronger baseline | Old outcome | New outcome |
|---|---|---|---|---|---|---|
| Li et al. | 941 | 2D incompressible Navier-Stokes | Pseudo-spectral 64x64 | Discontinuous Galerkin Order 2 7x7 | 1,000-times faster | 7-times faster |
| Lu et al. | 911 | 1D Advection | Finite-difference nx=100 | Discontinuous Galerkin Order 2 nx=13 | 24-times faster | 10-times slower |
| Kochkov et al. | 429 | 2D incompressible Navier-Stokes | Finite Volume | Pseudo-spectral | 80-times faster | Slightly slower |
| Bar-Sinai et al. | 382 | 1D Burgers’ equation | Weighted Essentially Non-Oscillatory | Discontinuous Galerkin Order 2/3 | 4–8-fold fewer degrees of freedom | 2–4-fold fewer degrees of freedom |
| Wang et al. | 230 | 1D Burgers’ equation | Spectral nx=100 | Finite Volume nx=100 | 1,000-times faster | 10-times slower |
| Li et al. | 124 | 2D incompressible Navier-Stokes | Pseudo-spectral 64x64 | Discontinuous Galerkin Order 2 3x3 | 1,000-times faster | 7-times faster |
| Hsieh et al. | 101 | 2D Poisson | Multigrid | Lower–Upper decomposition | Faster | 1,000-times slower |
| Brandstetter et al. | 87 | 1D Burgers’ equation, 1D Wave | Weighted Essentially Non-Oscillatory, Pseudo-spectral | Weighted Essentially Non-Oscillatory, Finite Volume | Much faster | 1,000-times slower |
| de Lara and Ferrer | 12 | 2D Poisson | Discontinuous Galerkin Order 28 nx=1 | Discontinuous Galerkin Order 9 nx=1 | 22–75-times faster | 4–10-times slower |
| Tang et al. | 2 | 2D Poisson | Conjugate Gradient and Multigrid | Lower–Upper decomposition | 12-times faster | 35–500-times slower |
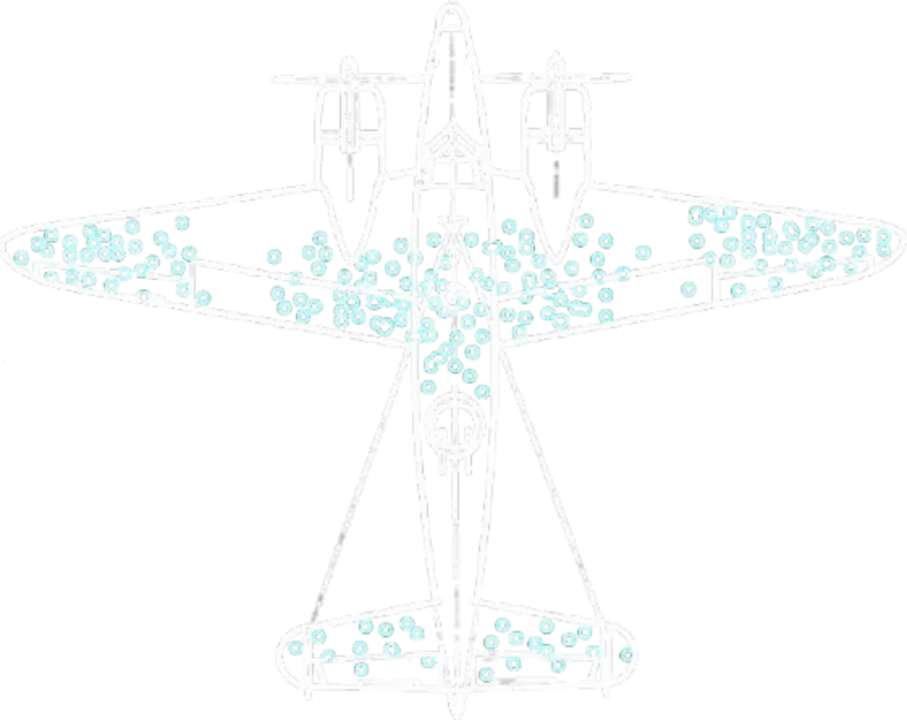
(Survivorship bias. Dots stand for places where surviving planes were shot. We find all these human remains in caves,
therefore early humans must have live primarily in caves. Credit: Martin Grandjean (vector), McGeddon (picture), US Air Force (hit plot concept).)
Initiation and Guessing
Next: To be continued