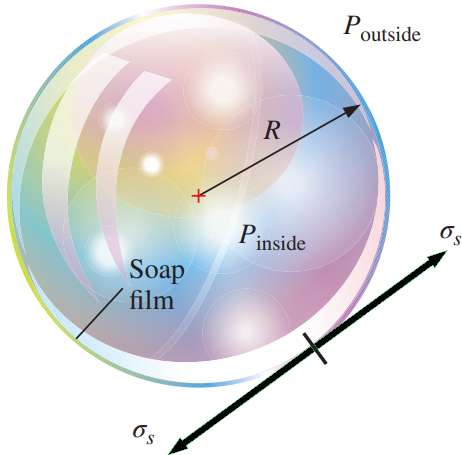
(1) Some children are playing with soap bubbles, and you become curious as to the relationship between soap bubble radius and the pressure inside the soap bubble. You reason that the pressure inside the soap bubble must be greater than atmospheric pressure, and that the shell of the soap bubble is under tension, much like the skin of a balloon. You also know that the property surface tension must be important in this problem. Not knowing any other physics, you decide to approach the problem using dimensional analysis. Establish a relationship between pressure difference \(\Delta P = P_{\text{inside}} - P_{\text{outside}}\), soap bubble radius \(R\), and the surface tension \(\sigma_s\) of the soap film.

The pressure inside a soap bubble is greater than that surrounding the soap bubble due to surface tension in the soap film.

(2) List the seven primary dimensions. What is significant about these seven?

(3) Explain the law of dimensional homogeneity in simple terms.