The dimensionless Mach number is defined as \[ \text{Ma} = \frac{V}{c} = \frac{\text{Speed of flow}}{\text{Speed of sound}} \] where $c$ is the speed of sound, whose value is 346 m/s in air at room temperature at sea level. A flow is called sonic when Ma = 1, subsonic when Ma < 1, supersonic when Ma > 1, and hypersonic when Ma ≫ 1.

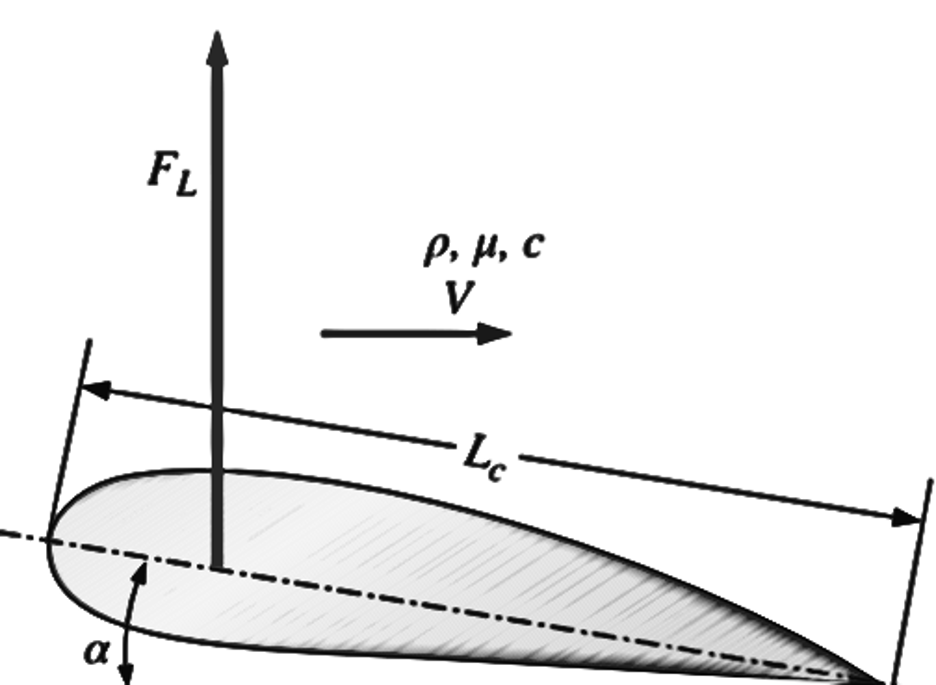
(1) Some aeronautical engineers are designing an airplane and wish to predict the lift produced by their new wing design. The chord length \(L_c\) of the wing is 1.12 m, and its planform area \(A\) (area viewed from the top when the wing is at zero angle of attack) is 10.7 m². The prototype is to fly at \(V = 52.0 \, \text{m/s}\) close to the ground where \(T = 25^\circ \text{C}\). They build a one-tenth scale model of the wing to test in a pressurized wind tunnel. The wind tunnel can be pressurized to a maximum of 5 atm. At what speed and pressure should they run the wind tunnel in order to achieve dynamic similarity?

Lift \(F_L\) on a wing of chord length \(L_c\) at angle of attack \(\alpha\) in a flow of free-stream speed \(V\) with density \(\rho\), viscosity \(\mu\), and speed of sound \(c\). The angle of attack \(\alpha\) is measured relative to the free-stream flow direction.

(2) A wind tunnel is used to measure the pressure distribution in the airflow over an airplane model. The air speed in the wind tunnel is low enough that compressible effects are negligible. The Bernoulli equation approximation is valid in such a flow situation everywhere except very close to the body surface or wind tunnel wall surfaces and in the wake region behind the model. Far away from the model, the air flows at speed \(V_\infty\) and pressure \(P_\infty\), and the air density \(\rho\) is approximately constant. Gravitational effects are generally negligible in airflows, so we write the Bernoulli equation as \[ P + \frac{1}{2} \rho V^2 = P_\infty + \frac{1}{2} \rho V_\infty^2 \] Nondimensionalize the equation, and generate an expression for the pressure coefficient \(C_p\) at any point in the flow where the Bernoulli equation is valid. \(C_p\) is defined as \[ C_p = \frac{P - P_\infty}{\frac{1}{2} \rho V_\infty^2} \]