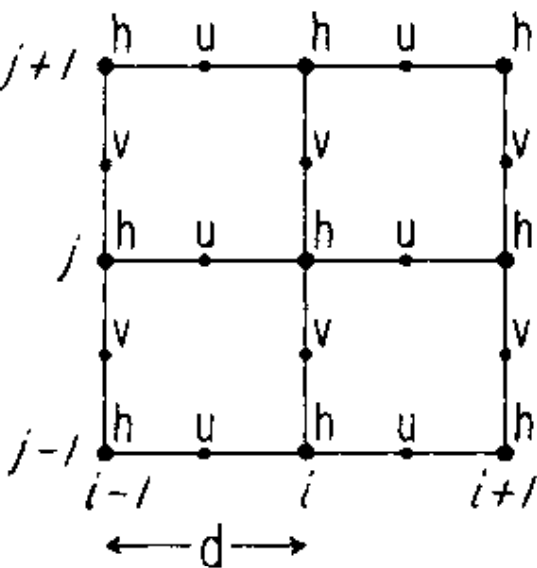
The basic algorithm employed for stepping forward the momentum equations is based on retaining non-divergence of the flow at all times. This is most naturally done if the components of flow are staggered in space in the form of an Arakawa C grid.

(1) Create a 2D scalar field on a square grid (e.g., a Gaussian bump). Write a function to compute the Laplacian using central finite differences. Use a uniform 100×100 grid over \([-1,1]\), apply second-order centered differences for \(\frac{\partial^2}{\partial x^2}\) and \(\frac{\partial^2}{\partial y^2}\), and visualize both the input field and the computed Laplacian. You can use matplotlib.pyplot.contourf or imshow to plot both the scalar field and its Laplacian side by side.

(2) Initialize a 2D velocity field representing a shear or vortex flow. Write a function to compute the vorticity field using finite differences, and plot the result with a colormap. Use vorticity = ∂v/∂x - ∂u/∂y, implement centered differences for spatial derivatives, and plot the vorticity field using imshow or contourf with labeled axes and colorbar.

(3) Initialize a passive tracer field and advect it in a constant 2D velocity field (e.g., \(u = 1, v = 0\)). Use an explicit time-stepping scheme and finite differences, then create an animation to visualize the tracer's evolution. Implement the advection equation \(\frac{\partial q}{\partial t} + u \frac{\partial q}{\partial x} + v \frac{\partial q}{\partial y} = 0\) using either upwind or central differencing, apply periodic boundaries manually, and plot the tracer field using matplotlib.animation.FuncAnimation.