Although things now become somewhat complicated algebraically, the effect of the damping term must create a new set of stable fixed points above the dashed lines
Some plots for different values of \(r\)

- When \( r_s < r < 0 \), both the origin and the new large-amplitude fixed points are stable. The initial condition determines the final outcome. Thus the origin is stable to small perturbations, but not to large perturbations
- Jumps. When \( r \) is increased to \( r = 0 \), the system jumps to a large-amplitude fixed point
- Hysteresis. If \( r \) is then decreased, the system stays on the large amplitude branch until it reaches \( r_s \), and then it jumps back to the origin. The dynamics are not reversible
- As \( r \) is increased past \( r_s \) from below, both an unstable and a stable fixed point appear, below and above the origin
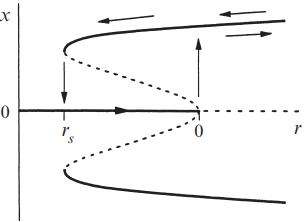
A major difference between the supercritical and subcritical pitchfork bifurcation is that the former leads to continuous changes \( x^* \sim \sqrt{r} \) as \( r \) is increased past zero, whereas the latter results in a finite jump. Because the jump can be quite large, subcritical bifurcations are sometimes called hard or dangerous, while supercritical bifurcations are called soft or safe
In the analogy with phase transitions, supercritical bifurcations are related to continuous or second-order phase transitions (e.g., the ferromagnetic transition), while subcritical bifurcations are discontinuous or first-order (e.g., the freezing of water into ice)
1Strogatz, S.H. (2015). Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering (2nd ed.). CRC Press.
2Daniel Rothman. (2022). Nonlinear Dynamics: Chaos. MIT OpenCourseWare.