In the supercritical case \(\boxed{\dot{x} = r x - x^3}\), the cubic term is stabilizing: it acts as a restoring force that pulls \( x(t) \) back toward \( x = 0 \). If instead the cubic term were destabilizing, as in \( \boxed{\dot{x} = r x + x^3}, \) then we'd have a subcritical pitchfork bifurcation
The non-zero fixed points \( x^* = \pm \sqrt{-r} \) are now unstable, and they exist only for \( r < 0 \). (Thus we see some reason for the name “subcritical”) The flows are now flipped compared to previously
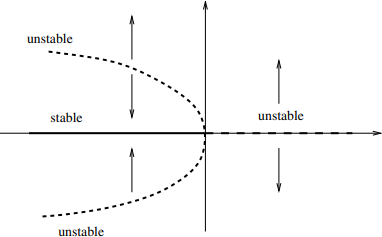
Subcritical pitchfork diagram
now the cubic term drives trajectories out to \( \pm\infty \), so still need a stabilizing term. The lowest-order nonlinear term that still maintains symmetry is then \( x^5 \), leading to the normal form \(\boxed{ \dot{x} = r x + x^3 - x^5} \)
1Strogatz, S.H. (2015). Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering (2nd ed.). CRC Press.
2Seydel, R. (2010). Practical Bifurcation and Stability Analysis. Interdisciplinary Applied Mathematics, vol 5. Springer, New York, NY.