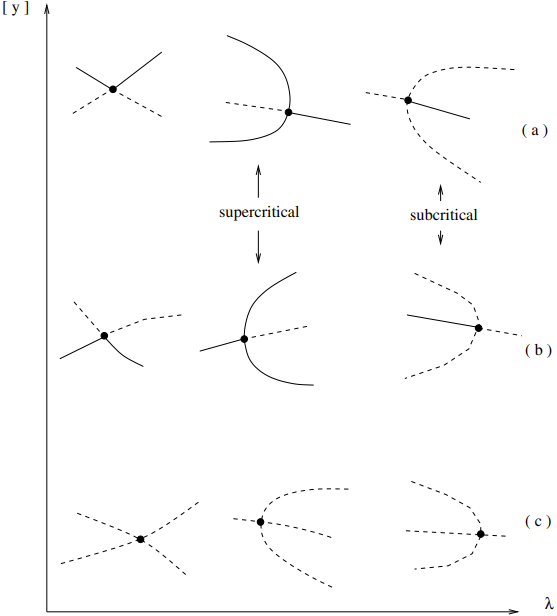
Stability at bifurcations (solid line for stable solutions)

A hysteresis phenomenon may collapse into a situation like that shown in (a), this kind of branch point is called a hysteresis point or cusp point
In (b) bifurcation point where more than two branches intersect is called a multiple bifurcation point
In (c) an isola center is depicted (also called point of isola formation). A neighboring solution cannot be found to the right or to the left of an isola center

The simplest equations that represent a certain type of bifurcation are called normal forms. The normal forms of the bifurcations discussed so far: \[ \begin{aligned} 0 &= \lambda \pm y^2 && \text{turning point, fold bifurcation} \\ 0 &= \lambda y \pm y^2 && \text{transcritical bifurcation} \\ 0 &= \lambda y \pm y^3 && \text{pitchfork bifurcation} \end{aligned} \]

¹Seydel, R. (2010). Practical Bifurcation and Stability Analysis. Interdisciplinary Applied Mathematics, vol 5. Springer, New York, NY.