Steady Flow between Parallel Plates
$$
u(y) = \frac{U}{h} y - \frac{1}{2\mu} \frac{dp}{dx}\, y \,(h-y)
$$
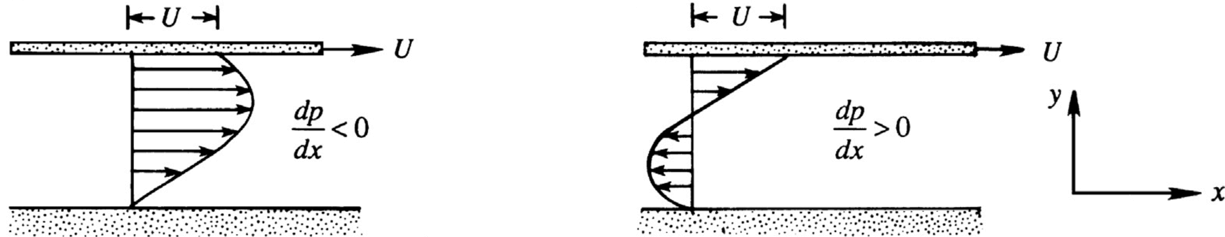
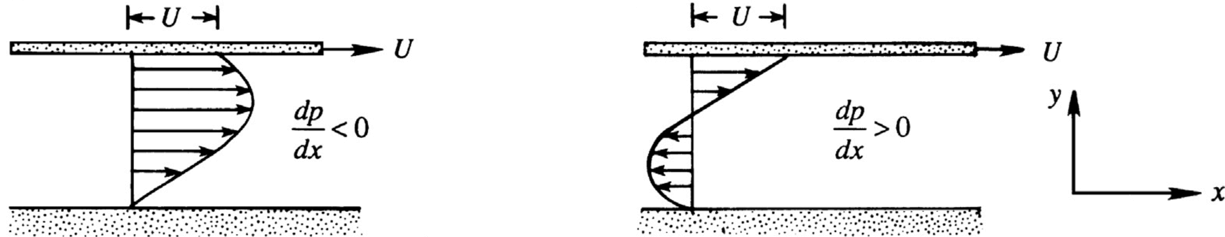
★ Volume flow rate per unit width of channel
$$
q = \int_{0}^{h} u \, dy
= \frac{U h}{2} \left[ 1 - \frac{h^2}{6 \mu U} \frac{dP}{dx} \right]
$$
\(\rightarrow\) Average velocity
$$
\bar{V} = \frac{q}{h}
= \frac{1}{h} \int_{0}^{h} u \, dy
= \frac{U}{2} \left[ 1 - \frac{h^2}{6 \mu U} \frac{dP}{dx} \right]
$$
Special cases
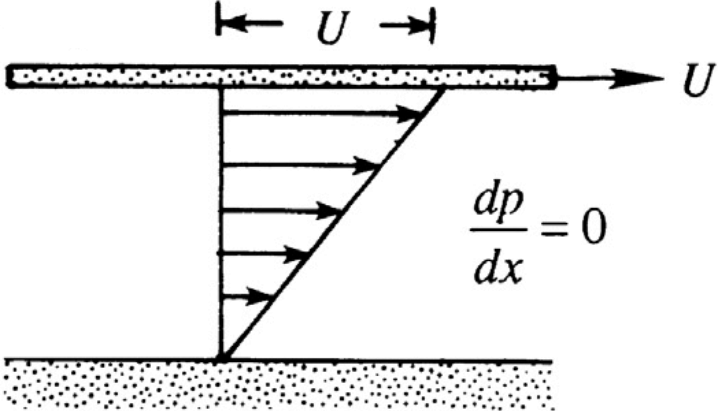

◀
▶
Plane Couette flow $$ \frac{dP}{dx} = 0 \rightarrow u(y) = \frac{U y}{h} $$

Plane Poiseuille flow $$ U = 0 \rightarrow u(y) = -\frac{1}{2\mu} \frac{dP}{dx} \; y (h - y) $$
