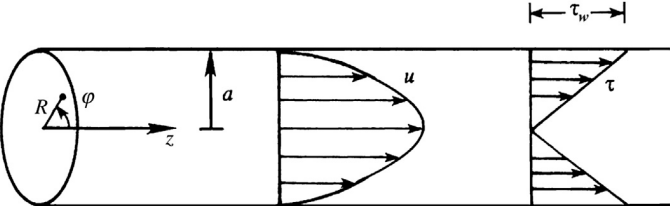
Steady Flow in a Round Tube (Circular Poiseuille Flow)
Use cylindrical coordinates $(R, \varphi, z)$
$$
\mathbf{u} = (0, 0, u_z(R))
$$
$\varphi, R, z$ momentum equations
$$
0 = \frac{\partial p}{\partial \varphi},
\quad 0 = \frac{\partial p}{\partial R},
\quad 0 = -\frac{dp}{dz} + \frac{\mu}{R} \frac{d}{dR} \left( R \frac{du_z}{dR} \right)
$$
$$
\Rightarrow u_z(R) = \frac{R^2}{4\mu} \frac{dp}{dz} + A \ln R + B
$$
Boundary conditions
- @ $R = a:\; u_z = 0$
- @ $R = 0:\; u_z$ is bounded
Volume flow rate
$$
Q = \int_0^a u(R)\, 2\pi R \, dR
= -\frac{\pi a^4}{8\mu} \frac{dp}{dz}
$$
Average velocity
$$
V = \frac{Q}{\pi a^2}
= -\frac{a^2}{8\mu} \frac{dp}{dz}
$$
 ◀
▶
◀
▶