$$ \mathbf{u} = (0, u_\varphi(R), 0) $$ $$ -\frac{u_\varphi^2}{R} = -\frac{1}{\rho}\frac{dP}{dR}, \quad 0 = \mu \frac{d}{dR} \left[ \frac{1}{R} \frac{d}{dR} \left( R u_\varphi \right) \right] $$ $$ \Rightarrow u_\varphi(R) = A R + \frac{B}{R} $$

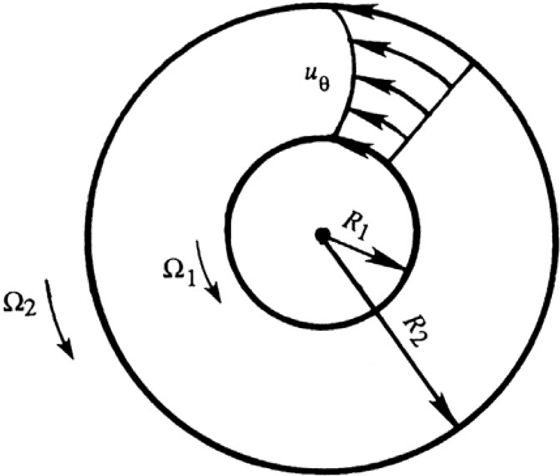
Boundary conditions

• @ $R = R_1:\; u_\varphi = \Omega_1 R_1$
• @ $R = R_2:\; u_\varphi = \Omega_2 R_2$

From boundary conditions $$ A = \frac{\Omega_2 R_2^2 - \Omega_1 R_1^2}{R_2^2 - R_1^2}, \quad B = -\frac{(\Omega_2 - \Omega_1) R_1^2 R_2^2}{R_2^2 - R_1^2} \Rightarrow u_\varphi(R) = \frac{1}{R_2^2 - R_1^2} \left\{ \big[ \Omega_2 R_2^2 - \Omega_1 R_1^2 \big] R - \big[ \Omega_2 - \Omega_1 \big] \frac{R_1^2 R_2^2}{R} \right\} $$