Steady Flow between Concentric Rotating Cylinders (Circular Couette Flow)
★Two special limits
$R_2 \to \infty$ & $\Omega_2 = 0$
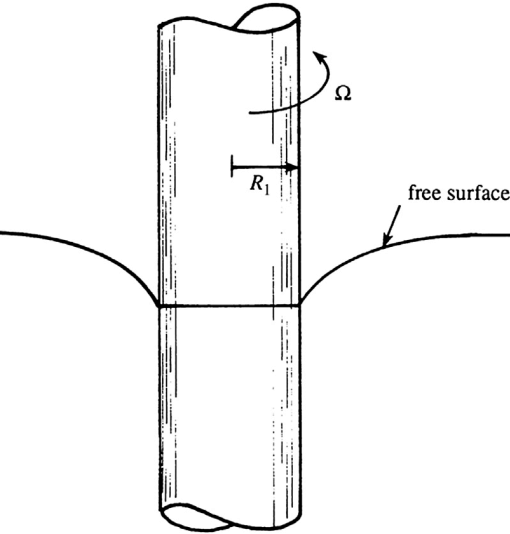

Flow outside a cylinder rotating in an infinite bath of fluid $$ u_\varphi = \frac{\Omega_1 R_1^2}{R} $$ Viscous shear stress $$ \sigma_{R\varphi} = \mu \left[ \frac{1}{R}\frac{\partial u_\varphi}{\partial \varphi} + R \frac{\partial}{\partial R} \left( \frac{u_\varphi}{R} \right) \right] = - \frac{2 \mu \Omega_1 R_1^2}{R^2} $$ Mechanical power supplied to fluid $$ (2 \pi R_1) \, \tau_{R\varphi} \, u_\varphi $$
$R_2 \to \infty$ & $\Omega_2 = 0$
Flow within a cylindrical tank $$ u_\varphi(R) = \Omega_2 R $$ Velocity field of solid body rotation
◀
▶
Flow within a cylindrical tank $$ u_\varphi(R) = \Omega_2 R $$ Velocity field of solid body rotation