Steady Flow between Parallel Plates
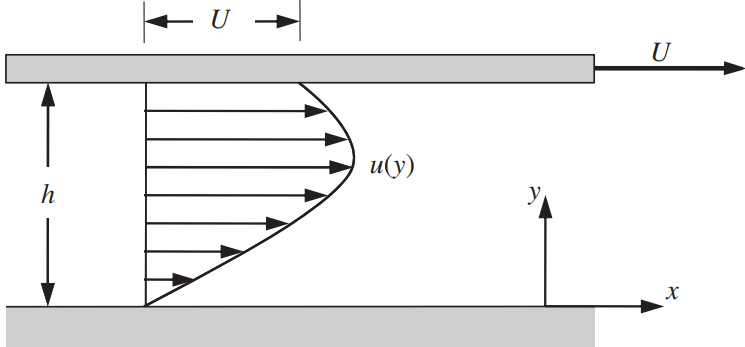
Fully developed flow \(\rightarrow \mathbf{u} = (u, v), \quad u = u(y)\)
$$
\frac{\partial u}{\partial x} = 0
\quad \xrightarrow{\text{continuity equation}} \boldsymbol{\nabla}\!\cdot\!\mathbf{u}
= \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0
\;\;\Rightarrow\;\; \frac{\partial v}{\partial y} = 0
\;\;\xrightarrow[v=0]{@\,y=0}\;\;\; v=0
$$
x-momentum:
$
0 = -\frac{1}{\rho}\frac{\partial p}{\partial x} + \nu \frac{\partial^2 u}{\partial y^2}
\;\;\;\longrightarrow\;\;\;
\frac{\partial p}{\partial x} = \text{const.} = \frac{dp}{dx}
$
y-momentum: $ 0 = -\frac{1}{\rho}\frac{\partial p}{\partial y} \;\;\;\longrightarrow\;\;\; \frac{\partial p}{\partial y} = 0 \;\;\;\longrightarrow\;\;\; p = p(x) $
y-momentum: $ 0 = -\frac{1}{\rho}\frac{\partial p}{\partial y} \;\;\;\longrightarrow\;\;\; \frac{\partial p}{\partial y} = 0 \;\;\;\longrightarrow\;\;\; p = p(x) $
$$
\frac{dP}{dx}=\text{const}
\;\;\xrightarrow{\text{x-mom}}\;\;
0=-\frac{y^{2}}{2}\frac{dP}{dx}
+\underbrace{\rho\,\nu}_{\mu}\,u
+A y + B
$$
A, B are determined from boundary conditions @ y = 0: u = 0 @ y = h: u = U
$$
\Longrightarrow\;\;
u(y) = \frac{U}{h} y - \frac{1}{2\mu} \frac{dp}{dx}\, y \,(h-y)
$$
◀
▶