Because of the presence of the nonlinear acceleration term \( \boxed{\mathbf{u} \cdot \nabla \mathbf{u}} \) in \(D \mathbf{u} / Dt = - (1 / \rho) \nabla p + \nu \nabla^2 \mathbf{u}\), very few exact solutions of the Navier-Stokes equations are known in closed form
An example of an exact solution is that for steady laminar flow between infinite parallel plates. Such a flow is said to be fully developed when its velocity profile \( u(x, y) \) becomes independent of the downstream coordinate \( x \), so that \( u = u(y) \) alone
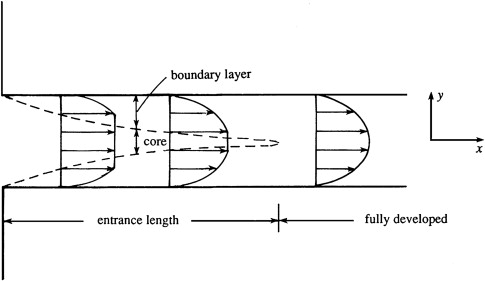
The entrance length of the flow, where the velocity profile depends on the downstream distance, may be several or even many times longer than the spacing between the plates
Within the entrance length, the derivative \( \frac{\partial u}{\partial x} \) is not zero, so the continuity equation \(\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0\) requires that \( v \ne 0 \), so that the flow is not parallel to the walls within the entrance length