Considering a sheet of inviscid fluid with constant and uniform density. The height of the surface of the fluid above the reference level $z = 0$ is $h(x, y, t)$. With application to the earth's atmosphere or ocean in mind, we model the body force arising from the potential $\Phi$ as a vector, $g$, directed perpendicular to the $z = 0$ surface. The rotation axis of the fluid coincides with the $z$-axis in the model, i.e., $\Omega = k\Omega$, so that in this case the Coriolis parameter $f$ is simply $2\Omega$. The rigid bottom is defined by the surface $z = h_B(x,y)$. The velocity has components $u, v,$ and $w$ parallel to the $x$-, $y$-, and $z$-axes respectively

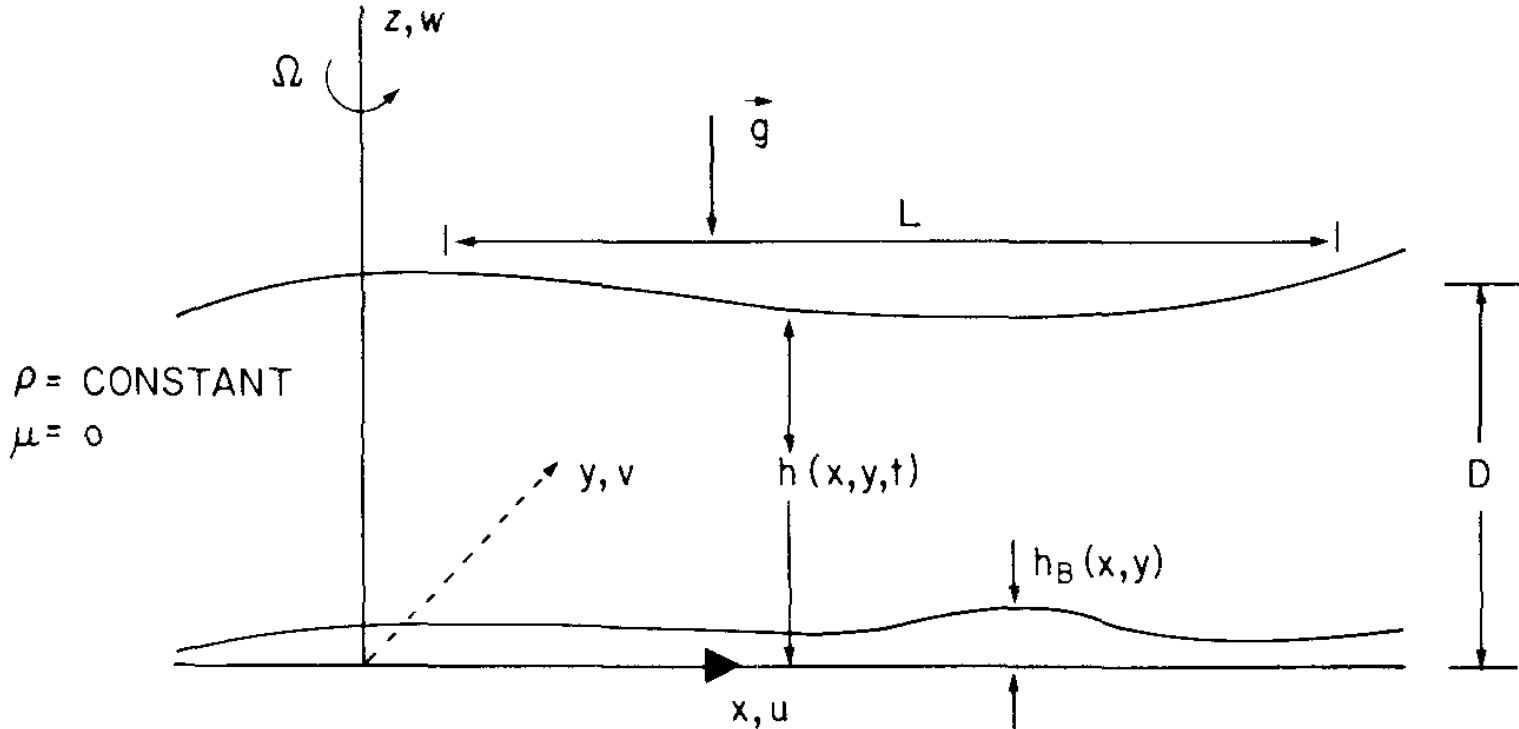
Although the depth of the fluid $h - h_B$ varies in space and time, we suppose that a characteristic value for the depth $D$ could be chosen, to be the average depth of the layer. We also suppose that $D$ characterizes the vertical scale of the motion as well. Similarly, we suppose there exists a characteristic horizontal length scale for the motion, which we call $L$. The fundamental parametric condition which characterizes shallow-water theory is $$ \delta = \frac{D}{L} \ll 1 $$