Shallow-Water Modelling
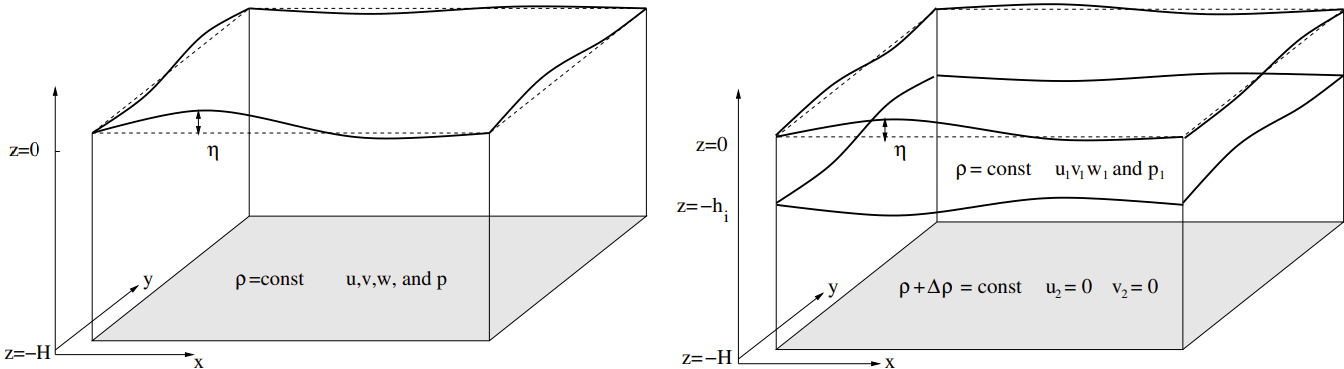
- Linear "barotropic" and "baroclinic" layered model for $f = 0$ in 1D $$ \frac{\partial u}{\partial t} = -g \frac{\partial h}{\partial x}, \qquad \frac{\partial h}{\partial t} + H \frac{\partial u}{\partial x} = 0 $$
- $h$ is total thickness ("barotropic") or layer interface $h_i$ ("baroclinic")
- Either $g = 9.81 \, \text{m/s}^2$ ("barotropic") or $g \to g \Delta \rho / \rho_0$ ("baroclinic")
- The linearized 1D shallow water equations (for $f = 0$) are $$ \frac{\partial u}{\partial t} = - \frac{\partial h}{\partial x}, \quad \frac{\partial h}{\partial t} = -c^2 \frac{\partial u}{\partial x} $$
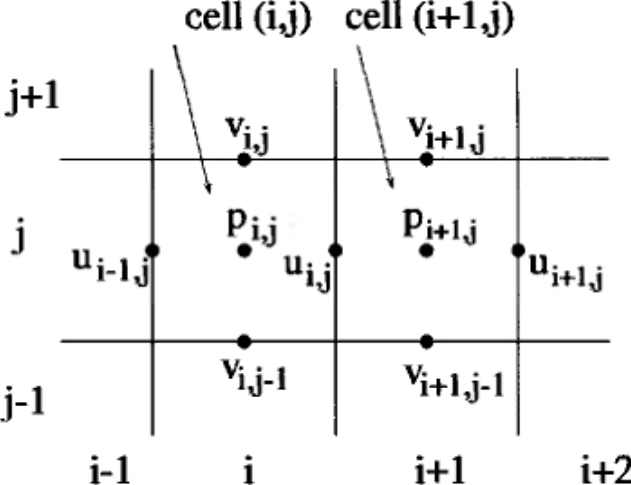
- Discrete version for staggered grid $$ \frac{d u_n}{dt} = -\delta^+ h_n, \quad \frac{d h_n}{dt} = -c^2 \delta^- u_n $$
- With the finite differencing operators $$ \delta^+ h_n = \frac{h_{n+1} - h_n}{\Delta}, \quad \delta^- h_n = \frac{h_n - h_{n-1}}{\Delta} $$
- Wave ansatz $ u_n = \hat{u}(t) e^{ikx}, \quad h_n = \hat{h}(t) e^{ikx}$ with $x = n\Delta, \; n=0,1,\dots $ $$ \delta^+ h_n = \hat{h} e^{ikn\Delta} \frac{(e^{ik\Delta} - 1)}{\Delta}, \qquad \delta^- u_n = \hat{u} e^{ikn\Delta} \frac{(1 - e^{-ik\Delta})}{\Delta} $$
1Markus Jochum and Carsten Eden. Bornö Summerschool 2024.