When numerical calculations take as their starting point the relevant equations of motion rather than simply evaluating an analytically derived formula, the calculation is usually termed a numerical experiment
It should be noted that in most cases the relevant partial differential equations are solved by representing derivatives by finite-difference approximations of varying degrees of accuracy. These finite-difference approximations require the repetitive evaluation of the dynamic variables on a spatial grid whose spacing between the points must be fine enough to resolve the fields properly. The grid cannot be too fine, however, for then the computation burden becomes excessive, both technologically and economically. There have been several important numerical experiments which have generated solutions of the vorticity equation. 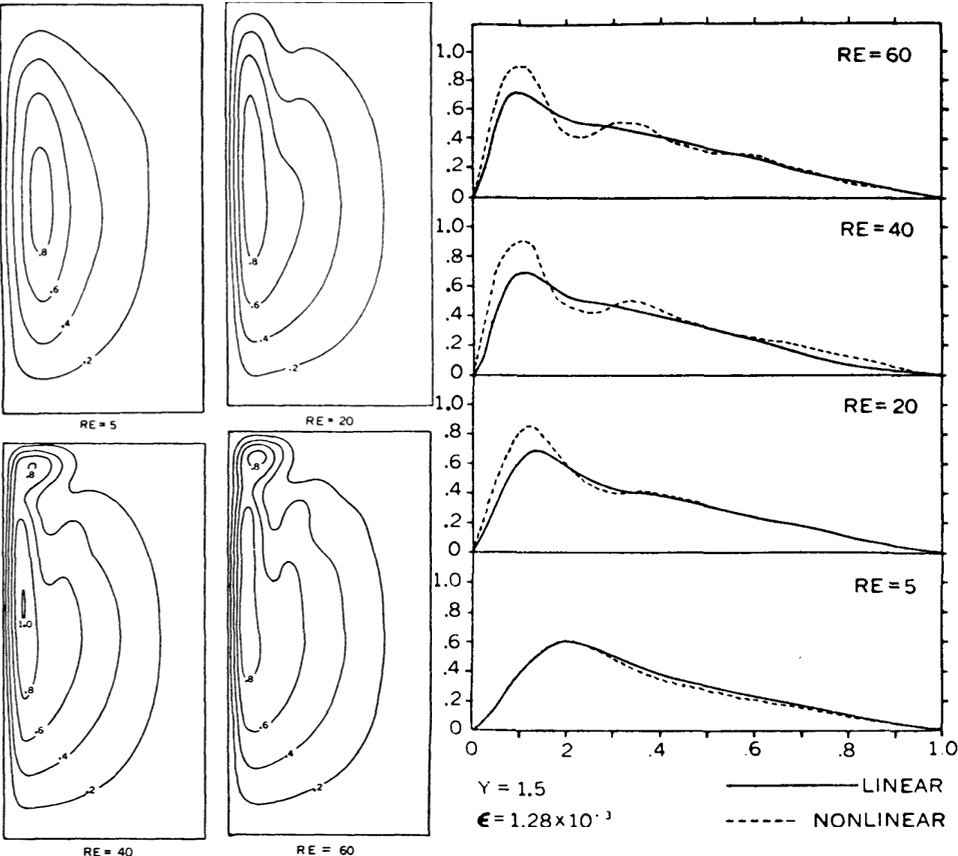For example, Bryan (1963) calculated the streamlines of the steady flow pattern with lateral friction, no bottom friction, and no-slip boundary conditions

◀ ▶