If \(\nabla \times \mathbf{u} \ne 0\) at every point in a flow,
the flow is called rotational.
This implies that the fluid elements have a finite angular velocity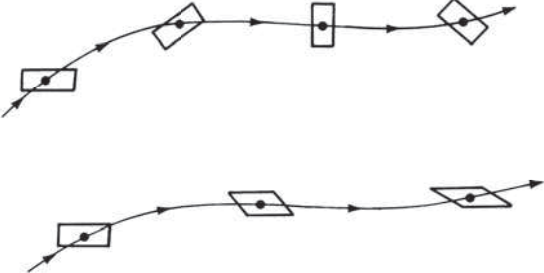
If \(\nabla \times \mathbf{u} = 0\) at every point in a flow,
the flow is called irrotational. This implies that the fluid elements have no angular velocity;
their motion through space is a pure translation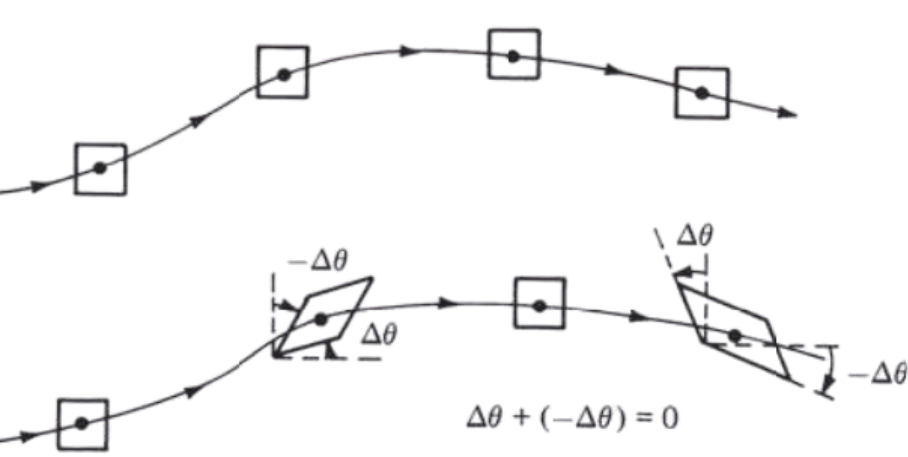
The angular velocity is typically denoted by \(\boldsymbol{\Omega}\) or \(\boldsymbol{\omega}\), while the vorticity is denoted by \(\boldsymbol{\xi}\) or also sometimes \(\boldsymbol{\omega}\), with the relationship \(\boldsymbol{\omega} = 2\boldsymbol{\Omega}\)
clarifying their connection in fluid dynamics. In this simple case, the vorticity is simply twice the angular velocity of the fluid
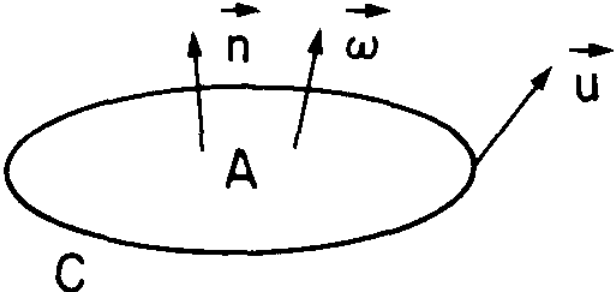
The generalization of this notion to the general case follows from Stokes’ theorem \[ \iint_A \boldsymbol{\omega} \cdot \mathbf{n} \, dA = \oint_C \mathbf{u} \cdot d\mathbf{r} \] where \(C\) is a contour enclosing the surface \(A\) whose normal at each point is \(\mathbf{n}\)
1 Anderson, John. (2017). Fundamentals of Aerodynamics, 6th ed. (6). New York: McGraw Hill Education.
2 Pedlosky, J. (1982). Geophysical Fluid Dynamics. Springer study edition. Springer, Berlin, Heidelberg.