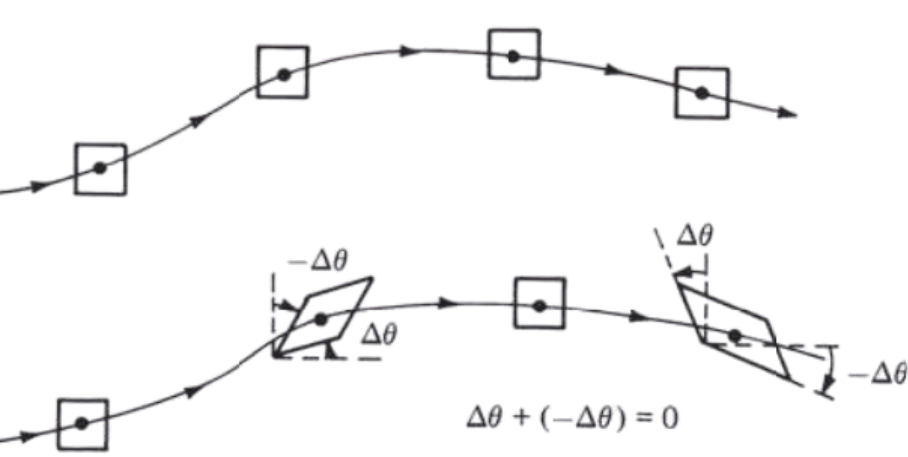
Let the angle between sides \(AB\) and \(AC\) be denoted by \(\kappa\). As the fluid element moves through the flow field, \(\kappa\) will change. At time \(t\), \(\kappa\) is initially \(90^\circ\). At time \(t + \Delta t\), \(\kappa\) has changed by the amount \(\Delta \kappa\) \[ \Delta \kappa = -\Delta \theta_2 - (-\Delta \theta_1) \] By definition, the strain of the fluid element as seen in the \(xy\) plane is the change in \(\kappa\), where positive strain corresponds to a decreasing \(\kappa\) \[ \text{Strain} = -\Delta \kappa = \Delta \theta_2 - \Delta \theta_1 \]

[Q] Consider the velocity field given by \( u = \frac{y}{x^2 + y^2}, v = \frac{-x}{x^2 + y^2} \), calculate the vorticity
[Sol] \( \boldsymbol{\omega} = \nabla \times \mathbf{u} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ \frac{y}{x^2 + y^2} & \frac{-x}{x^2 + y^2} & 0 \end{vmatrix} = \mathbf{i}[0 - 0] - \mathbf{j}[0 - 0] + \mathbf{k} \left[ \frac{(x^2 + y^2)(-1) + x(2x)}{(x^2 + y^2)^2} - \frac{(x^2 + y^2)(1) - y(2y)}{(x^2 + y^2)^2} \right]\\ = 0\mathbf{i} + 0\mathbf{j} + 0\mathbf{k} = 0 \) The flow field is irrotational at every point except at the origin, where \(x^2 + y^2 = 0\)