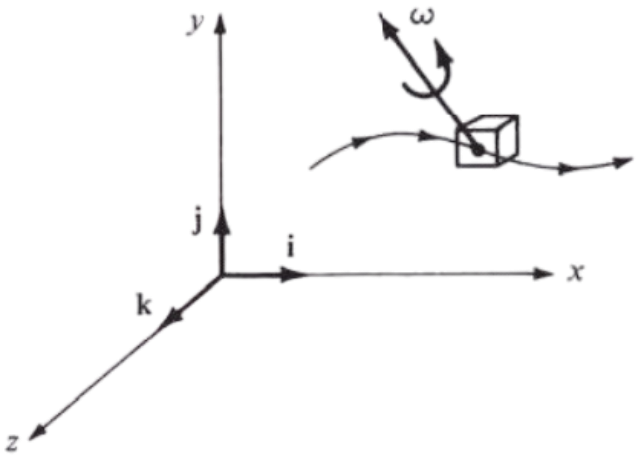
The resulting angular velocity of the fluid element in three-dimensional space is \[ \boldsymbol{\omega} = \omega_x \mathbf{i} + \omega_y \mathbf{j} + \omega_z \mathbf{k} \] \[\boxed{ \boldsymbol{\omega} = \frac{1}{2} \left[ \left( \frac{\partial w}{\partial y} - \frac{\partial v}{\partial z} \right) \mathbf{i} + \left( \frac{\partial u}{\partial z} - \frac{\partial w}{\partial x} \right) \mathbf{j} + \left( \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y} \right) \mathbf{k} \right]} \] It expresses the angular velocity of the fluid element in terms of derivatives of the velocity field

Denote vorticity by the vector \( \boldsymbol{\xi} \): \[ \boldsymbol{\xi} \equiv 2 \boldsymbol{\omega} \] \[ \boldsymbol{\xi} = \left( \frac{\partial w}{\partial y} - \frac{\partial v}{\partial z} \right) \mathbf{i} + \left( \frac{\partial u}{\partial z} - \frac{\partial w}{\partial x} \right) \mathbf{j} + \left( \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y} \right) \mathbf{k} \] Recall \(\boxed{\nabla \times \mathbf{u} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ u_x & u_y & u_z \end{vmatrix} = \mathbf{i} \left( \frac{\partial u_z}{\partial y} - \frac{\partial u_y}{\partial z} \right) + \mathbf{j} \left( \frac{\partial u_x}{\partial z} - \frac{\partial u_z}{\partial x} \right) + \mathbf{k} \left( \frac{\partial u_y}{\partial x} - \frac{\partial u_x}{\partial y} \right)}\) for \( \nabla \times \mathbf{u} \) in Cartesian coordinates. Since \( u \), \( v \), and \( w \) denote the \( x \)-, \( y \)-, and \( z \)-components of velocity \[ \boldsymbol{\xi} = \nabla \times \mathbf{u} \]