In the limit \( \Delta t \rightarrow 0 \), \[ \lim_{\Delta t \to 0} \frac{\Delta \mathbf{A}}{\Delta t} = \frac{d \mathbf{A}}{dt} = |\mathbf{A}| \sin \gamma \, \frac{d\theta}{dt} \, \frac{\boldsymbol{\Omega} \times \mathbf{A}}{|\boldsymbol{\Omega} \times \mathbf{A}|} \] \[\because |\boldsymbol{\Omega} \times \mathbf{A}| = |\boldsymbol{\Omega}| \, |\mathbf{A}| \sin \gamma \Rightarrow \boxed{ \frac{d \mathbf{A}}{dt} = \boldsymbol{\Omega} \times \mathbf{A} } \] for a vector of fixed magnitude

An observer who is fixed in the rotating frame of reference would see no change in \( \mathbf{A} \), while an observer in a nonrotating frame would see \( \mathbf{A} \) change as described by \(\boxed{ \frac{d \mathbf{A}}{dt} = \boldsymbol{\Omega} \times \mathbf{A} }\). Both observers would see the same vector \( \mathbf{A} \), since by definition a vector \( \mathbf{A} \) is independent of the coordinate frame used to describe it. However, their perceptions of the rate of change of \( \mathbf{A} \) differ markedly. Since \[ \frac{d |\mathbf{A}|^2}{dt} = 2 \mathbf{A} \cdot \frac{d \mathbf{A}}{dt} = 2 \mathbf{A} \cdot ( \boldsymbol{\Omega} \times \mathbf{A} ) = 0 \] both observers agree that the magnitude of \( \mathbf{A} \) is unaltered

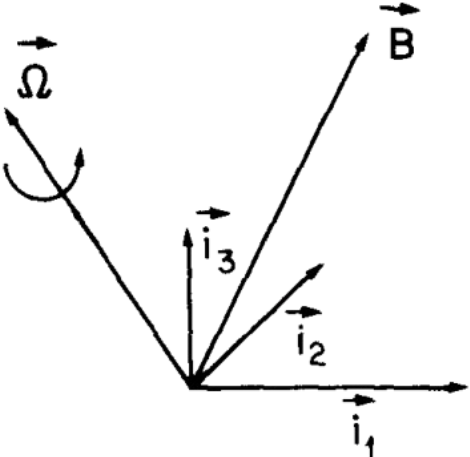
Vector in rotating frame: \( \mathbf{B} = B_1 \mathbf{i}_1 + B_2 \mathbf{i}_2 + B_3 \mathbf{i}_3 \)
Component definition (projection of \( \mathbf{B} \) along basis vectors): \( B_j = \mathbf{i}_j \cdot \mathbf{B}, j = 1, 2, 3 \)
Time derivative of a vector in rotating frame: \( \left( \frac{d \mathbf{B}}{dt} \right)_R = \frac{d B_1}{dt} \mathbf{i}_1 + \frac{d B_2}{dt} \mathbf{i}_2 + \frac{d B_3}{dt} \mathbf{i}_3 \) (The time rate of change of \( \mathbf{B} \))

¹ Pedlosky, J. (1982). Geophysical Fluid Dynamics. Springer study edition. Springer, Berlin, Heidelberg.