More About Rotating Coordinate Frames
Most natural frame from which to describe atmospheric and oceanic motions
is one which rotates with the planetary angular velocity \( \boldsymbol{\Omega} \). To an observer in a rotating frame objects fixed in inertial space will appear
to rotate and, because of the curvature of their apparent trajectory, to be accelerating
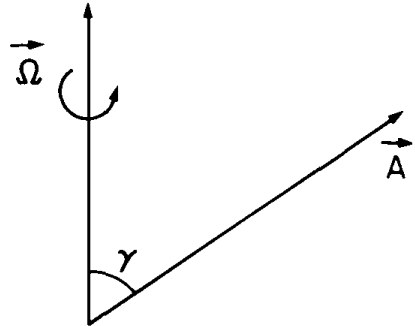
Let \( \boldsymbol{\Omega} \) be the angular velocity vector, and \( \mathbf{A} \) a vector of constant magnitude rotating with \( \boldsymbol{\Omega} \). The angle between \( \mathbf{A} \) and \( \boldsymbol{\Omega} \) is denoted by \( \gamma \)
In a small time interval \( \Delta t \), the vector \( \mathbf{A} \) rotates through an angle\(\Delta \theta = |\boldsymbol{\Omega}| \, \Delta t\)
where \( |\boldsymbol{\Omega}| \) is the magnitude of the angular velocity vector
First-order approximation of vector change
\[
\mathbf{A}(t + \Delta t) - \mathbf{A}(t) \equiv \Delta \mathbf{A} = \mathbf{n} |\mathbf{A}| \sin \gamma \, \Delta \theta + \mathcal{O}((\Delta \theta)^2)
\]
Unit vector in direction of change (perpendicular to both \(\mathbf{A}\) and \(\boldsymbol{\Omega}\))
\[
\mathbf{n} = \frac{\boldsymbol{\Omega} \times \mathbf{A}}{|\boldsymbol{\Omega} \times \mathbf{A}|}
\]
1 Pedlosky, J. (1982). Geophysical Fluid Dynamics. Springer study edition. Springer, Berlin, Heidelberg.