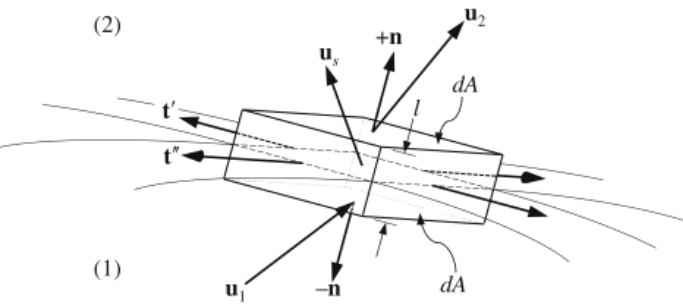
The mass conservation result, obtained from the control volume and Reynolds Transport Theorem applied to mass conservation in a control volume moving with velocity \(\mathbf{b} = \mathbf{u}_s\) \(\boxed{\frac{d}{dt} \int_{V^*(t)} \rho(\mathbf{x}, t) \, dV + \int_{A^*(t)} \rho(\mathbf{x}, t) \left( \mathbf{u}(\mathbf{x}, t) - \mathbf{b} \right) \cdot \mathbf{n} \, dA = 0}\) is \[ \dot{m}_s = \rho_1 (\mathbf{u}_1 - \mathbf{u}_s) \cdot \mathbf{n} = \rho_2 (\mathbf{u}_2 - \mathbf{u}_s) \cdot \mathbf{n} \] where \(\dot{m}_s\) is the surface mass flux per unit area

Importantly, only the normal component \((\mathbf{u}_s \cdot \mathbf{n})\) of \(\mathbf{u}_s\) enters this boundary condition formulation. Thus \(\mathbf{u}_s\) can be chosen with arbitrary or convenient tangential components, and this feature allows simplifications when curved moving interfaces are studied using Cartesian coordinates

If medium 1 is a fluid that is immiscible with fluid 2, then no mass flows across the boundary, \(\dot{m}_s = 0\), and \(\dot{m}_s = \rho_1 (\mathbf{u}_1 - \mathbf{u}_s) \cdot \mathbf{n} = \rho_2 (\mathbf{u}_2 - \mathbf{u}_s) \cdot \mathbf{n}\) reduces to \(\mathbf{u}_1 \cdot \mathbf{n} = \mathbf{u}_s \cdot \mathbf{n}\) and \(\mathbf{u}_2 \cdot \mathbf{n} = \mathbf{u}_s \cdot \mathbf{n}\)
If medium 1 is a solid that is not dissolving, subliming, ablating, or otherwise emitting material at the interface, then \(\mathbf{u}_1 = \mathbf{u}_s\) so \(\dot{m}_s\) is again zero, and the conservation of mass boundary condition reduces to \(\mathbf{u}_2 \cdot \mathbf{n} = \mathbf{u}_s \cdot \mathbf{n}\)
In addition, if the solid is stationary then \(\mathbf{u}_2 \cdot \mathbf{n} = 0\)

In general, \(\dot{m}_s = \rho_1 (\mathbf{u}_1 - \mathbf{u}_s) \cdot \mathbf{n} = \rho_2 (\mathbf{u}_2 - \mathbf{u}_s) \cdot \mathbf{n}\) must be used without simplification when there is mass-flow through a moving surface, as in the case of a moving shockwave observed from a stationary vantage point