On a solid boundary or at the interface between two immiscible fluids, some of the necessary boundary conditions may be derived from the conservation laws by examining a small thin control volume that spans the interface
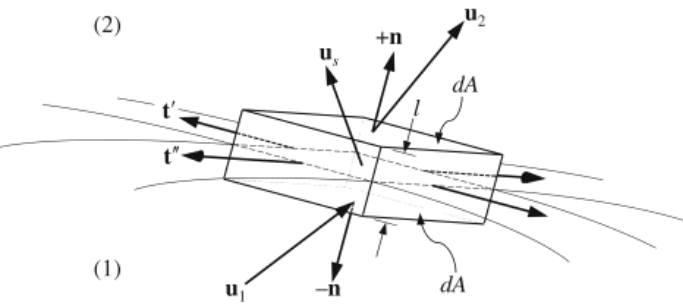
For a control volume as shown in the figure, the interface separating medium 2 (a fluid) from medium 1 (a solid or a fluid immiscible with fluid 2). This control volume moves with the interface's velocity \(\mathbf{u}_s\). When necessary, \(\mathbf{u}_s\) can be developed from a specification of the shape of the interface.
\(+\mathbf{n}\) and \(-\mathbf{n}\) are the unit normal vectors pointing into medium 2 and medium 1. The square surfaces of the control volume have area \(dA\), are locally parallel to the interface, and are separated from each other by a small distance \(l\). The two tangent vectors to the surface are \(\mathbf{t}'\) and \(\mathbf{t}''\), and are chosen so that \(\mathbf{t}' \times \mathbf{t}'' = \mathbf{n}\)
Application of the conservation laws to the rectangular volume \(l\,dA\) as \(l \to 0\), keeping the two square area elements in the two different media, produces five boundary conditions. As \(l \to 0\), all volume integrals \(\to 0\) and the surface integrals over the four rectangular side areas, which are proportional to \(l\), tend to zero unless there is interfacial (surface) tension
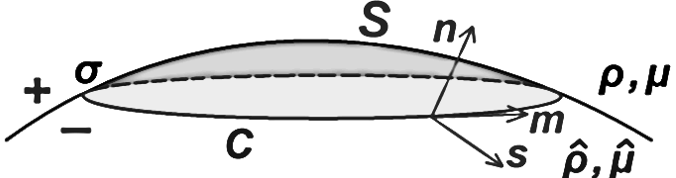
The normal and tangential stress boundary conditions appropriate at a fluid–fluid interface characterized by an interfacial tension \(\sigma\)
There is a surface \(S\) and bounding contour \(C\) on an interface between two fluids. Local unit vectors are \(\mathbf{n}\), \(\mathbf{m}\), and \(\mathbf{s}\)
1 Prof. John W. M. Bush. MIT OpenCourseWare: 18.357 Interfacial Phenomena