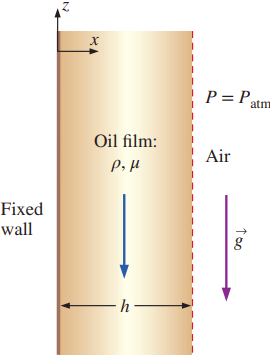
[Q] Consider steady, incompressible, parallel, laminar flow of a film of oil falling slowly down an infinite vertical wall. The oil film thickness is \(h\), and gravity acts in the negative \(z\)-direction.
There is no applied (forced) pressure driving the flow—the oil falls by gravity alone. Calculate the velocity and pressure fields in the oil film and sketch the normalized velocity profile. You may neglect changes in the hydrostatic pressure of the surrounding air
[Sol] The flow is assumed to occur along an infinite wall in a steady, parallel, incompressible Newtonian, and laminar system, with constant pressure, 2D velocity, and gravity downward
The boundary conditions are There is no slip at the wall; at \(x = 0\), \(u = v = w = 0\)
At the free surface \((x = h)\), there is negligible shear, which for a vertical free surface in this coordinate system means \(\partial w / \partial x = 0\) at \(x = h\)
\(\therefore\) Fully developed flow, incompressible continuity equation \(\cancel{\underbrace{\frac{\partial u}{\partial x}}_{\text{Parallel flow}}} + \cancel{\underbrace{\frac{\partial v}{\partial y}}_{\text{Two-dimensional}}} + \frac{\partial w}{\partial z} = 0 \quad \rightarrow \quad \frac{\partial w}{\partial z} = 0\)
Result of continuity is \(w = w(x) \) only
\(\quad \because\) \( u = v = 0 \) everywhere, and gravity does not act in the \( x \)- or \( y \)-directions
\(\therefore\) \(\rho \left(
\underbrace{\cancel{\frac{\partial w}{\partial t}}}_{\text{Steady flow}} +
\underbrace{\cancel{u \frac{\partial w}{\partial x}}}_{\text{Parallel flow}} +
\underbrace{\cancel{v \frac{\partial w}{\partial y}}}_{\text{Two-dimensional}} +
\underbrace{\cancel{w \frac{\partial w}{\partial z}}}_{\text{continuity}}
\right)
=
- \underbrace{\frac{\partial p}{\partial z}}_{\text{Constant pressure}} +
\underbrace{\rho g_z}_{-\rho g}
+ \mu \left(
\frac{d^2 w}{d x^2} +
\underbrace{\cancel{\frac{\partial^2 w}{\partial y^2}}}_{\text{Two-dimensional}} +
\underbrace{\cancel{\frac{\partial^2 w}{\partial z^2}}}_{\text{continuity}}
\right) \\
\quad \Rightarrow \quad
\boxed{\frac{d^2 w}{d x^2} = \frac{\rho g}{\mu}}\)
\(\because\) If \( u = u(x) \) only, change from PDE to ODE \( \frac{\partial u}{\partial x} \rightarrow \frac{d u}{d x}\)
\(\therefore\) Solve the differential equations \(w = \frac{\rho g}{2\mu} x^2 + C_1 x + C_2\)
\(\therefore\) Apply boundary conditions, \(
w = 0 + 0 + C_2 = 0 \Rightarrow C_2 = 0\) and \(\left( \frac{d w}{d x} \right)_{x = h} = \frac{\rho g}{\mu} h + C_1 = 0 \Rightarrow C_1 = -\frac{\rho g h}{\mu}\)
\(\therefore\) Velocity field \(w = \frac{\rho g}{2 \mu} x^2 - \frac{\rho g}{\mu} h x = \frac{\rho g x}{2 \mu} (x - 2h)\)
\(\because\) \( x < h \) in the film, \( w \) is negative everywhere as the flow is downward \(\therefore\) The pressure field is \(P = P_{\text{atm}}\) everywhere
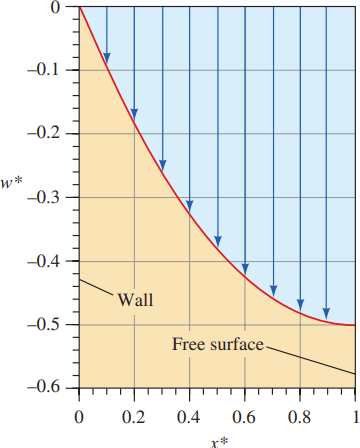
\(\therefore\) Let \( x^* = x/h \) and \( w^* = w \mu / (\rho g h^2) \), normalized velocity profile \(w^* = \frac{x^*}{2} (x^* - 2)\)
1 Fluid Mechanics: Fundamentals and Applications Fourth Edition. Çengel and J. M. Cimbala, McGraw-Hill, New York (2018).