Let's Have More Boundary Conditions
For the case of a liquid in contact with a gas with negligible surface tension effects, the free-surface boundary conditions are \[ P_{\text{liquid}} = P_{\text{gas}} \quad \text{and} \quad \tau_{s,\, \text{liquid}} \approx 0 \]
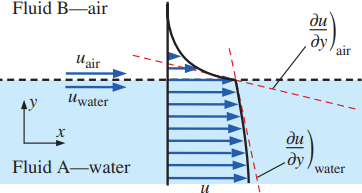
WaterAirFreeSurfaceBoundary

A degenerate form of the interface boundary condition occurs at the free surface of a liquid, meaning that fluid A is a liquid and fluid B is a gas (usually air). Boundary conditions at water–air interface: \[ u_{\text{water}} = u_{\text{air}} \quad \text{and} \quad \tau_{s,\, \text{water}} = \mu_{\text{water}} \left( \frac{\partial u}{\partial y} \right)_{\text{water}} = \tau_{s,\, \text{air}} = \mu_{\text{air}} \left( \frac{\partial u}{\partial y} \right)_{\text{air}} \]

Dynamic viscosity \(\mu_{\text{water}}\) is over 50 times greater than \(\mu_{\text{air}}\) ViscosityTableAccording to the Newton’s law of viscosity \(\tau_s = \mu \left( \frac{\partial u}{\partial y} \right)\), in order for the shear stresses to be equal, Boundary conditions at water–air interface requires that slope \((\partial u / \partial y)_{\text{air}}\) be more than 50 times greater than \((\partial u / \partial y)_{\text{water}}\). Since \(\mu_{\text{air}} \ll \mu_{\text{water}}\) a good approximation is that the shear stress at the water surface is negligibly small

Other boundary conditions arise depending on the problem setup. We often need to define inlet boundary conditions at a boundary of a flow domain where fluid enters the domain and outlet boundary conditions at an outflow. Symmetry boundary conditions are useful along an axis or plane of symmetry. For unsteady flow problems we also need to define initial conditions (at the starting time, usually \( t = 0 \))

1 Fluid Mechanics: Fundamentals and Applications Fourth Edition. Çengel and J. M. Cimbala, McGraw-Hill, New York (2018).

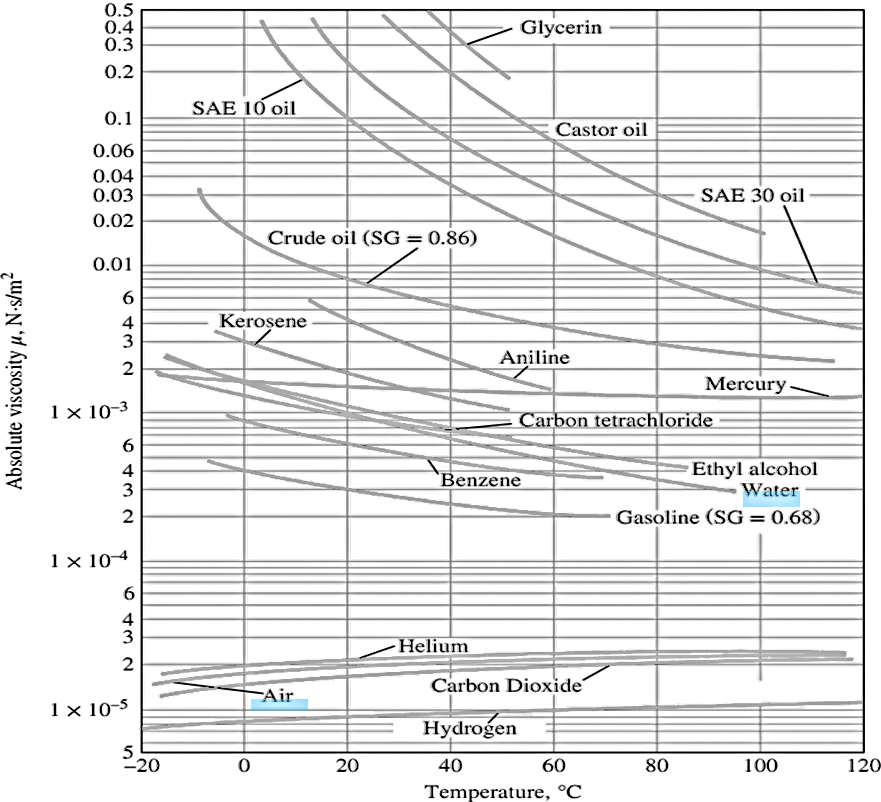
2 The figure variation of dynamic (absolute) viscosity of common fluids with temperature at 1 atm, \( (1 \, \text{N} \cdot \text{s}/\text{m}^2 = 1 \, \text{kg}/\text{m} \cdot \text{s}) \) is also Fluid Mechanics: Fundamentals and Applications Fourth Edition. Çengel and J. M. Cimbala, McGraw-Hill, New York (2018). Data from EES and F. M. White, Fluid Mechanics 7e

◀ ▶