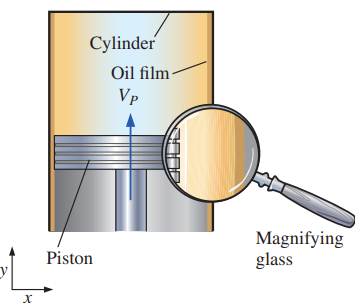
A special case is for a stationary wall with \(\vec{V}_{\text{wall}} = 0\); the fluid adjacent to a stationary wall has zero velocity, Consider the thin film of oil between a piston and its cylinder wall, from a stationary frame of reference, the fluid adjacent to the cylinder is at rest, and the fluid adjacent to the moving piston has velocity \(\vec{V}_{\text{fluid}} = \vec{V}_{\text{wall}} = V_p \vec{j}\). From a frame of reference moving with the piston, however, the fluid adjacent to the piston has zero velocity, but the fluid adjacent to the cylinder has velocity \(\vec{V}_{\text{fluid}} = \vec{V}_{\text{wall}} = -V_p \vec{j}\). An exception to the no-slip condition occurs in rarefied gas flows that the air can actually slip along the wall

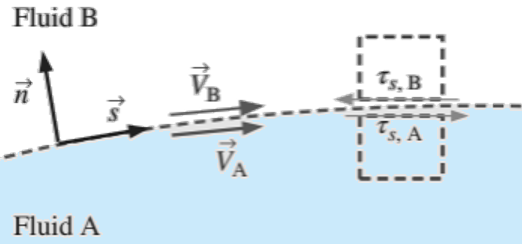
The shear stress \(\tau_s\) must also match between the two fluids. \(\tau_{s,A}\) is drawn on the top of the fluid particle in fluid A, while \(\tau_{s,B}\) is drawn on the bottom of the fluid particle in fluid B, and we have considered the direction of shear stress carefully. Because of the sign convention on shear stress, the direction of the arrows is opposite (Newton’s third law). Although velocity is continuous across the interface, its slope is not. If temperature effects are considered \(T_A = T_B\) at the interface, but there may be a discontinuity in the slope of temperature at the interface as well