Control Volume
The dot product of a second-order tensor and a vector yields a second vector; this operation is often called the contracted product or the inner product of a tensor and a vector.
In our case, it turns out that the inner product of the stress tensor \(\sigma_{ij}\) and the unit outward normal vector \(\vec{n}\) of a differential surface element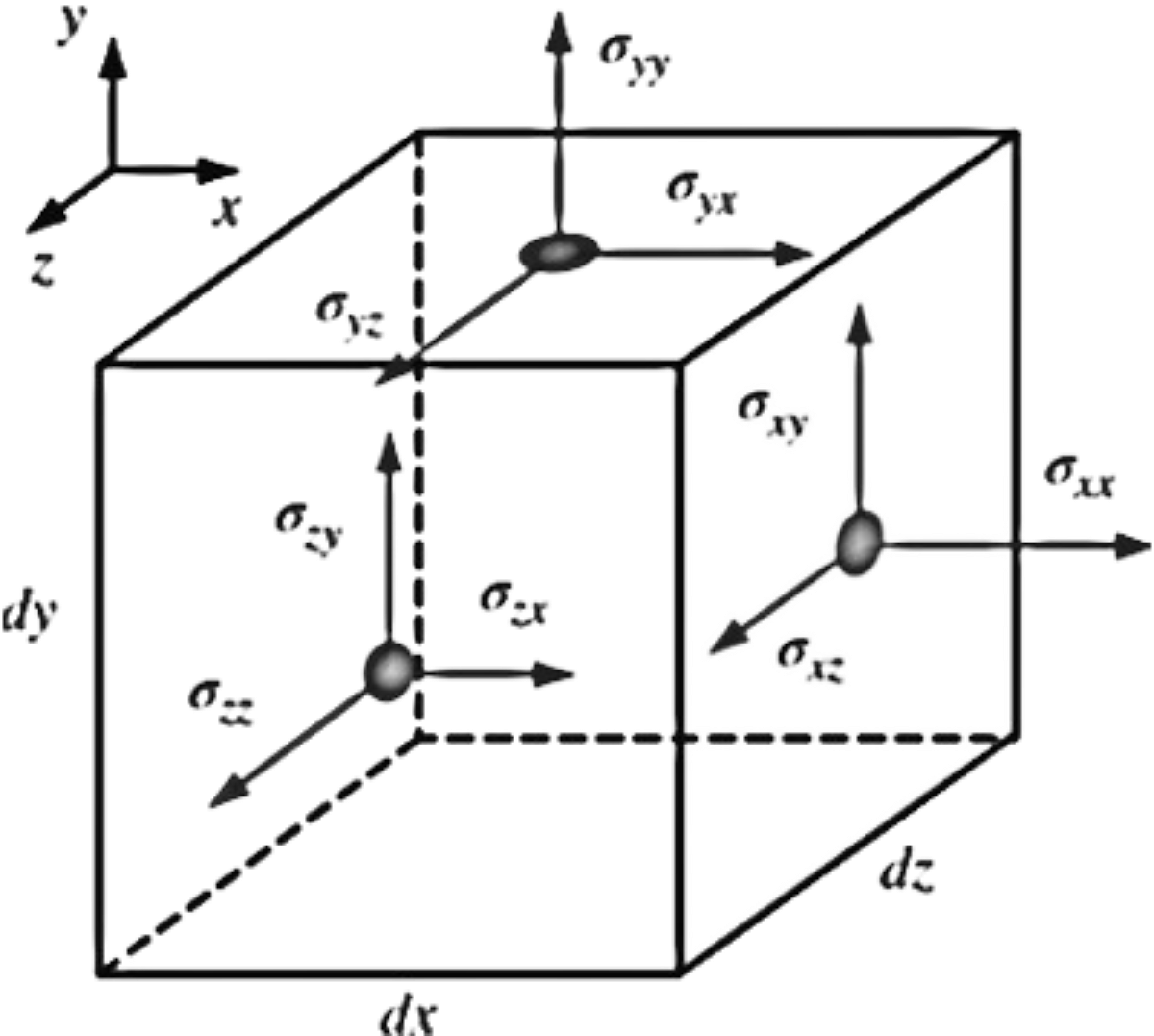
yields a vector whose magnitude is the force per unit area acting on the surface element and whose direction is the direction of the surface force itself
In our case, it turns out that the inner product of the stress tensor \(\sigma_{ij}\) and the unit outward normal vector \(\vec{n}\) of a differential surface element
yields a vector whose magnitude is the force per unit area acting on the surface element and whose direction is the direction of the surface force itself
Surface force acting on a differential surface element
\(
d\vec{F}_{\text{surface}} = \sigma_{ij} \vec{n} \, dA
\)
Total surface force acting on control surface
\(
\sum \vec{F}_{\text{surface}} = \int_{\text{CS}} \sigma_{ij} \vec{n} \, dA
\)
\(\boxed{\sum \vec{F}_{\text{body}} = \int_{\text{CV}} \rho \vec{g} \, dV = m_{\text{CV}} \vec{g}}\) and \(\boxed{\sum \vec{F}_{\text{surface}} = \int_{\text{CS}} \sigma_{ij} \vec{n} \, dA}\) into \( \boxed{\sum \vec{F} = \sum \vec{F}_{\text{body}} + \sum \vec{F}_{\text{surface}}}\)
\[
\sum \vec{F} = \sum \vec{F}_{\text{body}} + \sum \vec{F}_{\text{surface}} = \int_{\text{CV}} \rho \vec{g} \, dV + \int_{\text{CS}} \sigma_{ij} \vec{n} \, dA
\]
\[
\underbrace{\sum \vec{F}}_{\text{total force}} =
\underbrace{\sum \vec{F}_{\text{gravity}}}_{\text{body force}} +
\underbrace{\sum \vec{F}_{\text{pressure}} + \sum \vec{F}_{\text{viscous}} + \sum \vec{F}_{\text{other}}}_{\text{surface forces}}
\]
1Fluid Mechanics: Fundamentals and Applications Fourth Edition. Çengel and J. M. Cimbala, McGraw-Hill, New York (2018).