Newton’s second law for a system of mass \( m \) subjected to net force \( \sum \vec{F} \) is expressed as \[ \sum \vec{F} = m \vec{a} = m \frac{d \vec{V}}{dt} = \frac{d}{dt}(m \vec{V}) \] where \( m \vec{V} \) is the linear momentum of the system

Noting that both the density and velocity may change from point to point within the system, Newton’s second law can be expressed more generally as \[ \sum \vec{F} = \frac{d}{dt} \int_{\text{sys}} \rho \vec{V} \, dV \] where \( \rho \vec{V} \, dV \) is the momentum of a differential element \( dV \), which has mass \( \delta m = \rho \, dV \)

Therefore, Newton’s second law can be stated as the sum of all external forces acting on a system is equal to the time rate of change of linear momentum of the system. This statement is valid for a coordinate system that is at rest or moves with a constant velocity, called an inertial coordinate system or inertial reference frame. Accelerating systems such as aircraft during takeoff are best analyzed using noninertial (or accelerating) coordinate systems fixed to the aircraft

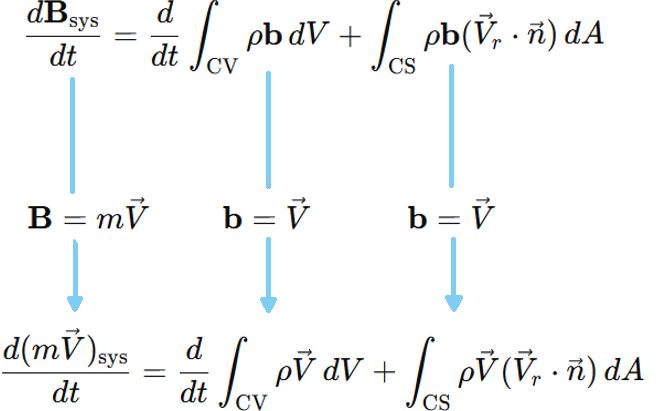
The Reynolds transport theorem provides the necessary tools to shift from the system formulation to the control volume formulation. Setting \( b = \vec{V} \) and thus \( B = m \vec{V} \), the Reynolds transport theorem is expressed for linear momentum as \[ \frac{d (m \vec{V})_{\text{sys}}}{dt} = \frac{d}{dt} \int_{\text{CV}} \rho \vec{V} \, dV + \int_{\text{CS}} \rho \vec{V} (\vec{V}_r \cdot \vec{n}) \, dA \] In general \(\boxed{ \sum \vec{F} = \frac{d}{dt} \int_{\text{CV}} \rho \vec{V} \, dV + \int_{\text{CS}} \rho \vec{V} (\vec{V}_r \cdot \vec{n}) \, dA} \)

\( \left( \begin{array}{c} \text{The sum of all} \\ \text{external forces} \\ \text{acting on a CV} \end{array} \right) = \left( \begin{array}{c} \text{The time rate of change} \\ \text{of the linear momentum} \\ \text{of the contents of the CV} \end{array} \right) + \left( \begin{array}{c} \text{The net flow rate of} \\ \text{linear momentum out of the} \\ \text{control surface by mass flow} \end{array} \right) \)

¹Fluid Mechanics: Fundamentals and Applications Fourth Edition. Çengel and J. M. Cimbala, McGraw-Hill, New York (2018).

◀ ▶