When the face is not parallel to one of the coordinate axes, mathematical laws for axes rotation and tensors can be used to calculate the normal and tangential components acting at the face. In addition, an alternate notation called tensor notation is convenient when working with tensors.
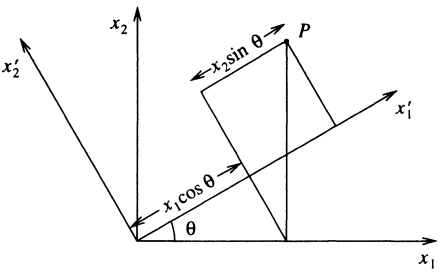
Consider a rotation of a two-dimensional Cartesian coordinate system \( x_1, x_2 \) through an angle \( \theta \) to give a new coordinate system \( x_1', x_2' \). The coordinates of a point \( P \) in the \( x_1, x_2 \) system are related to those in the \( x_1', x_2' \) system by the equations \[ x_1' = x_1 \cos \theta + x_2 \sin \theta \] \[ x_2' = x_2 \cos \theta - x_1 \sin \theta \] or in matrix form, \[ \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \]
The \(2 \times 2\) matrix relating \((x_1', x_2')\) to \((x_1, x_2)\) is
\(
L = \begin{pmatrix}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{pmatrix}
\)
The matrix multiplication can be written in suffix notation
\(\boxed{
x_1' = L_{11}x_1 + L_{12}x_2 = L_{1j}x_j, \quad
x_2' = L_{21}x_1 + L_{22}x_2 = L_{2j}x_j}
\)
or generally
\(\boxed{
x_i' = L_{ij}x_j}
\)
Inverse rotation (through \(-\theta\))
\(
L^{-1} = \begin{pmatrix}
\cos(-\theta) & \sin(-\theta) \\
-\sin(-\theta) & \cos(-\theta)
\end{pmatrix}
= \begin{pmatrix}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{pmatrix},
\)
which is the transpose of \(L\). Therefore
\(
L_{ij}L_{kj} = \delta_{ik}
\)
A matrix with this property, that its inverse is equal to its transpose, is said to be orthogonal,
the inverse of the transformation can be written down simply by transposing the suffixes
\(
x_i = L_{ji}x_j'
\)
Another important property of the matrix \(L\) is that its determinant is
\(\boxed{
|L| = \cos^2 \theta + \sin^2 \theta = 1}
\)
For \(\mathbf{x} = x_1 \mathbf{e}_1 + x_2 \mathbf{e}_2 + x_3 \mathbf{e}_3\), the \(i\) component is defined by
\(
x_i' = \mathbf{e}_i' \cdot \mathbf{x} = \mathbf{e}_i' \cdot \mathbf{e}_j x_j \Rightarrow \) \(L_{ij} = \mathbf{e}_i' \cdot \mathbf{e}_j
\)
So \(L_{ij}\) = cosine of angle between \(\mathbf{e}_i'\) and \(\mathbf{e}_j\). Inverse matrix is transpose again \(L_{ji}\)
Since \(LL^T = I\), orthogonality ensures \( |L|^2 = 1 \Rightarrow |L| = \pm 1 \)
\(+1\): rotation
\(-1\): reflection
Two further important properties of \(L\) follow
\(\boxed{
\frac{\partial x_i'}{\partial x_j} = L_{ij}, \quad \frac{\partial x_i}{\partial x_j'} = L_{ji}}
\)
1P. C. Matthews, Vector Calculus, New York:Springer-Verlag, 1998.