It can be specified in terms of two scalar functions \( \mathbf{\Psi} = \chi \nabla \psi \) Putting this specification for \( \mathbf{\Psi} \) into \(\rho \mathbf{u} = \nabla \times \mathbf{\Psi}\) produces \( \rho \mathbf{u} = \nabla \chi \times \nabla \psi, \) because the curl of any gradient is identically zero
[Q] Use Stokes’ theorem to prove that \( \nabla \times (\nabla \phi) = 0 \) for any single-valued twice-differentiable scalar \( \phi \) regardless of the coordinate system
[Pf] \(\because\) Stokes theorem \( \iint_A (\nabla \times \mathbf{u}) \cdot \mathbf{n} \, dA = \int_C \mathbf{u} \cdot \mathbf{t} \, ds \)
Let \( \mathbf{u} = \nabla \phi \) \(\because\) \( \mathbf{t} \) vector points along the contour \( C \) that has path increment \( ds \)
\(\therefore\) Note \( \nabla \phi \cdot \mathbf{t} \, ds = \left( \frac{\partial \phi}{\partial s} \right) ds = d\phi \)
\(\therefore\) \( \iint_A \left( \nabla \times \left[ \nabla \phi \right] \right) \cdot \mathbf{n} \, dA = \int_C \nabla \phi \cdot \mathbf{t} \, ds = \int_C d\phi = 0 \), the final equality holds for integration on a closed contour of a single-valued function \( \phi \)
\(\therefore\) For an arbitrary surface \( A \) of any size, shape, orientation, or location, this can only be true if \( \nabla \times (\nabla \phi) = 0 \)
If \( \nabla \times (\nabla \phi) \) were nonzero at some location, an area integration in a small region centered on this location would not be zero. Such a nonzero integral is not allowed, thus \( \nabla \times (\nabla \phi) = 0 \) must be zero everywhere because \( A \) is arbitrary

Furthermore, \( \nabla \chi \) is perpendicular to surfaces of constant \( \chi \), and \( \nabla \psi \) is perpendicular to surfaces of constant \( \psi \)
\(\Rightarrow\) the mass flux \( \rho \mathbf{u} = \nabla \chi \times \nabla \psi \) will be parallel to will be parallel to surfaces of constant \( \chi \) and constant \( \psi \)
\(\Rightarrow\) three-dimensional streamlines are the intersections of the two stream surfaces, or stream functions in a three-dimensional flow

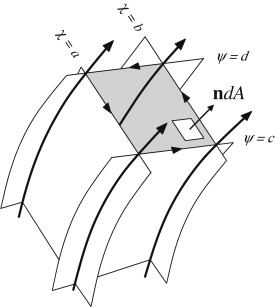
Consider two members of each of the families of the two stream functions \( \chi = a, \chi = b, \psi = c, \psi = d \)
The mass flux \( \dot{m} \) through the surface \( A \) bounded by the four stream surfaces is calculated with area element \( dA \), normal \( \mathbf{n} \), and Stokes’ theorem