Consider the steady form of the continuity equation \[ \nabla \cdot (\rho \mathbf{u}) = 0 \]
The divergence of the curl of any vector field is identically zero, so \( \rho \mathbf{u} \) will satisfy \(\nabla \cdot (\rho \mathbf{u}) = 0\) when written as the curl of a vector potential \( \mathbf{\Psi} \) \[ \rho \mathbf{u} = \nabla \times \mathbf{\Psi} \]
[Q] Use the vector integral theorems to prove that \( \nabla \cdot (\nabla \times \mathbf{u}) = 0 \) for any twice-differentiable vector function \( \mathbf{u} \) regardless of the coordinate system
[Pf]
\(\because\) Gauss’ theorem
\(
\iiint_V \nabla \cdot \mathbf{Q} \, dV = \iint_A \mathbf{n} \cdot \mathbf{Q} \, dA
\)
The arbitrary closed volume \( V \) has surface \( A \), and the outward normal is \( \mathbf{n} \)
Let \( \mathbf{Q} = \nabla \times \mathbf{u} \)
\(\therefore\)
\(
\iiint_V \nabla \cdot (\nabla \times \mathbf{u}) \, dV = \iint_A \mathbf{n} \cdot (\nabla \times \mathbf{u}) \, dA
\)
Split \( V \) into two sub-volumes \( V_1 \) and \( V_2 \), where the surface of \( V_1 \) is \( A_1 \) and the surface of \( V_2 \) is \( A_2 \), \( A_1 + A_2 = A \)
\(\therefore\)
\(
\iiint_V \nabla \cdot (\nabla \times \mathbf{u}) \, dV = \iint_{A_1} \mathbf{n} \cdot (\nabla \times \mathbf{u}) \, dA + \iint_{A_2} \mathbf{n} \cdot (\nabla \times \mathbf{u}) \, dA
\)
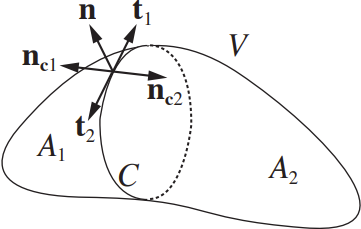
\(\because\) the bounding curve \( C \) for \( A_1 \) and \( A_2 \) is the same
\(\therefore\) Stokes’ theorem produces
\(
\iiint_V \nabla \cdot (\nabla \times \mathbf{u}) \, dV = \int_C \mathbf{u} \cdot \mathbf{t}_1 \, ds + \int_C \mathbf{u} \cdot \mathbf{t}_2 \, ds
\)
Here the tangent vectors \( \mathbf{t}_1 = \mathbf{n}_{c1} \times \mathbf{n} \) and \( \mathbf{t}_2 = \mathbf{n}_{c2} \times \mathbf{n} \) have opposite signs because \( \mathbf{n}_{c1} \) and \( \mathbf{n}_{c2} \), the normals to \( C \) that are tangent to surfaces \( A_1 \) and \( A_2 \) have opposite sign,
the two terms on the right side of the last equation are equal and opposite
\(\therefore\)
\(\boxed{
\iiint_V \nabla \cdot (\nabla \times \mathbf{u}) \, dV = 0}
\)
for an arbitrary closed volume of any size, shape, or location
This can only be true if \( \nabla \cdot (\nabla \times \mathbf{u}) = 0 \). If \( \nabla \cdot (\nabla \times \mathbf{u}) \) were nonzero at some location, then integration in a small volume centered on this location would not be zero, \( \nabla \cdot (\nabla \times \mathbf{u}) \) must be zero everywhere because \( V \) is arbitrary