Roughly speaking, fractals are complex geometric shapes with fine structure at arbitrarily small scales. Usually they have some degree of self-similarity. Fractals are of great interest because of their exquisite combination of beauty, complexity, and endless structure
Consider the logistic map
\(
x_{n+1} = r x_n (1 - x_n)
\)
for \(0 \leq x_n \leq 1\) and \(0 \leq r \leq 4\). Find all the fixed points and determine their stability
[Sol] The fixed points satisfy
\(
x^* = f(x^*) = r x^* (1 - x^*)
\)
Hence \(x^* = 0\) or
\(
1 = r(1 - x^*), \text{ i.e., } x^* = 1 - \frac{1}{r}.
\)
The origin is a fixed point for all \(r\), whereas \(x^* = 1 - \frac{1}{r}\) is in the range of allowable \(x\) only if \(r \geq 1\)
Stability depends on the multiplier
\(
f'(x^*) = r - 2rx^*.
\)
Since \(f'(0) = r\), the origin is stable for \(r < 1\) and unstable for \(r > 1\). At the other fixed point,
\(
f'(x^*) = r - 2r(1 - \frac{1}{r}) = 2 - r.
\)
Hence \(x^* = 1 - \frac{1}{r}\) is stable for \(-1 < (2 - r) < 1\), i.e., for \(1 < r < 3\). It is unstable for \(r > 3\)
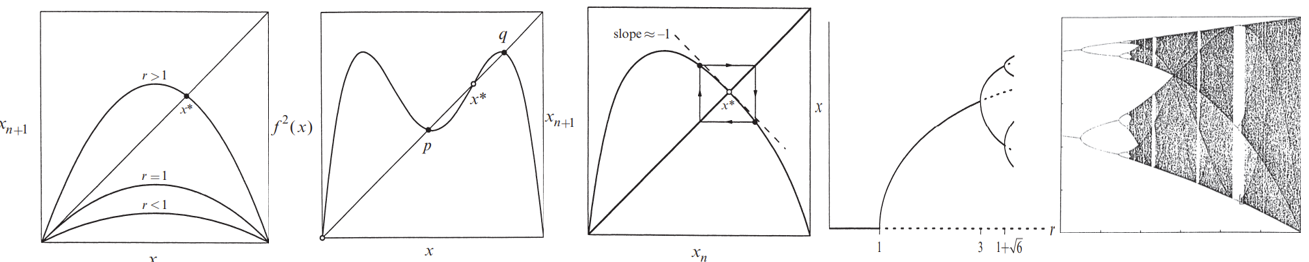
1Strogatz, S.H. (2015). Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering (2nd ed.). CRC Press.