The Lorenz equations have only two nonlinearities, the quadratic terms \(xy\) and \(xz\). There is also an important symmetry in the Lorenz system, the property or characteristic of the system of equations is that if a change of variable is made: \((x, y) \rightarrow (-x, -y)\), the equations stay the same. Hence, if \((x(t), y(t), z(t))\) is a solution, so is \((-x(t), -y(t), -z(t))\). In other words, all solutions are either symmetric themselves or have a symmetric partner
Lorenz used numerical integration to predict the trajectories in the long run. He studied the particular cases when \(\sigma = 10\), \(b = 8/3\), and \(r = 28\). This value of \(r\) is just above the Hopf bifurcation value of \( r_H = \sigma(\sigma + b + 3)/(\sigma - b - 1) \approx 24.74, \) which represents the critical point where a system's stability switches and a periodic solution arises. In general, the appearance or the disappearance of a periodic orbit through a local change in the stability properties of a steady point is known as the Hopf bifurcation
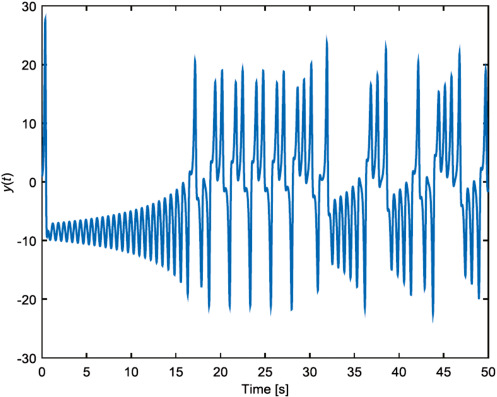
Behavior of \(y(t)\) of the Lorenz equations
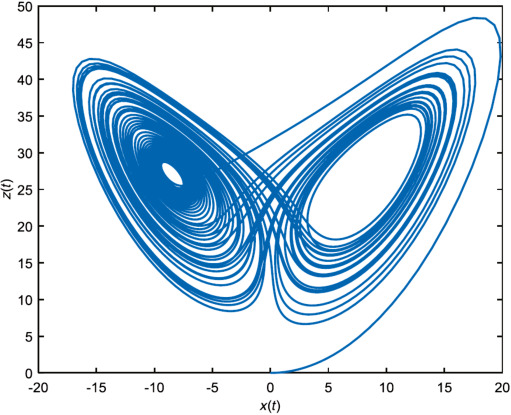
Butterfly pattern between \(x(t)\) and \(z(t)\)
1Gilberto Espinosa-Paredes. (2021). Fractional-Order Models for Nuclear Reactor Analysis.