
Suppose a 2D system has a stable fixed point.
What are possible ways it could lose stability as a parameter \(\mu\) varies?
The eigenvalues of the Jacobian are the key
If the fixed point is stable, the eigenvalues \(\lambda_1, \lambda_2\) must both lie in the left half-plane
Re \(\lambda < 0\). Either the eigenvalues are both real and negative or they are
complex conjugates. To destabilize the fixed point, one or both of the eigenvalues to cross into the right half-plane as \(\mu\) varies
Supercritical Hopf bifurcation: stable spiral becomes unstable spiral surrounded by a limit cycle
Physically: oscillations that decay in time become oscillations with constant amplitude in time
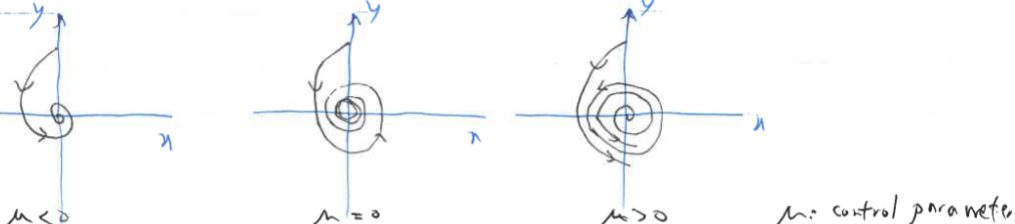
Subcritical Hopf bifurcation: unstable spiral shrinks & engulfs the origin which changes from a stable to an unstable fixed point

1Strogatz, S.H. (2015). Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering (2nd ed.). CRC Press.