Distinguishing Boundary Layer Separation from Turbulence

Boundary layer separation is the detachment of a boundary layer from the wall surface due to the adverse pressure gradient

One necessary condition for boundary layer separation is adverse pressure gradient
The other necessary condition for boundary layer separation is the viscous force, which retards the flow together with the adverse pressure gradient

Flow separation and turbulence are two completely different flow phenomena, and there is no necessary connection between them. The flow after separation can be laminar or turbulent, depending on the Reynolds number and the degree of deceleration within the boundary layer

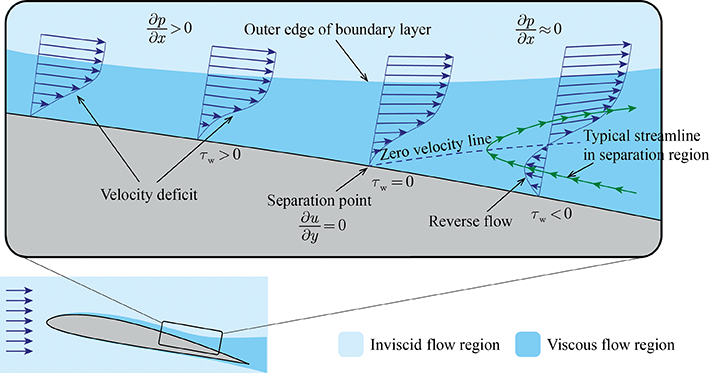
The upstream fluid moves forward, while the downstream fluid moves backward. Therefore, there must be a position where the streamwise velocity component becomes zero, known as the separation point $$ \left.\frac{\partial u}{\partial y}\right|_{\text{wall}} = 0 $$

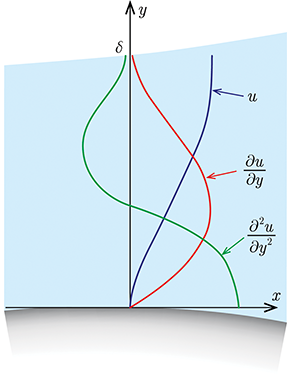
As long as no reverse flow occurs, we have $\partial u / \partial y > 0$ throughout the boundary layer. Therefore, the near-wall velocity gradient must increase from zero to some positive value, and the rate of change of the velocity gradient is positive. In other words, the second derivative of the velocity with respect to the coordinate normal to the flow is positive $$ \frac{\partial^{2} u}{\partial y^{2}} > 0 $$

¹Hongwei Wang (2023). A Guide to Fluid Mechanics. National Defense Industry Press.

◀ ▶