Kelvin-Helmholtz Instabilitys
Instability at the interface between two horizontal parallel fluid streams with different velocities and densities is called the Kelvin-Helmholtz instability.
This is an inertial instability and it can be readily analyzed assuming ideal flow in each stream. The name is also commonly used to describe the instability of the more general case where the variations of velocity and density are continuous and occur over a finite thickness
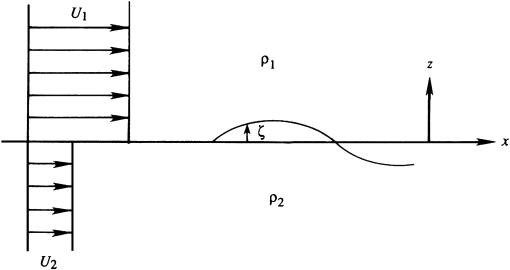
The Kelvin-Helmholtz instability is analyzed in two dimensions $(x, z)$,
where $x$ is the stream-wise coordinate and $z$ is the vertical coordinate.
Two fluid layers of infinite depth meet at a zero-thickness interface located at
$z = \zeta(x, t)$.
Let $U_1$ and $\rho_1$ be the horizontal velocity and density of the basic state in the upper half-space. Let $U_2$ and $\rho_2$ be those of the basic state in the lower half-space.
From Kelvin's circulation theorem, the perturbed flow must be irrotational in each half-space
The interface can be described by the velocity potentials
$$
\tilde{\phi}_1 =
\underbrace{U_1 x}_{\text{basic state}}
+
\underbrace{\phi_1}_{\text{perturbation}},
\qquad
\tilde{\phi}_2 =
\underbrace{U_2 x}_{\text{basic state}}
+
\underbrace{\phi_2}_{\text{perturbation}}
$$
$\tilde{\phi}_1$ and $\tilde{\phi}_2$ must satisfy the Laplace equation, so the perturbation potentials, $\phi_1$ and $\phi_2$, must also satisfy
$$
\nabla^2 \phi_1 = 0,
\qquad
\nabla^2 \phi_2 = 0
$$
◀
▶