Method of Normal Modes

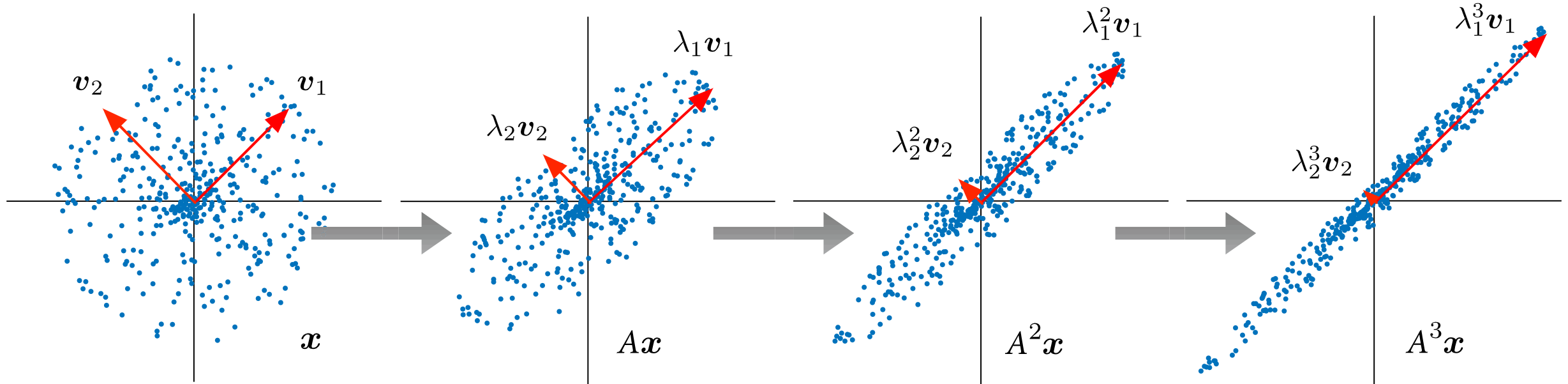
The method of analysis involving the examination of Fourier components is called the normal mode method. An arbitrary disturbance can be decomposed into a complete set of normal modes. In this method the stability of each of the modes is examined separately, as the linearity of the problem implies that the various modes do not interact. The method leads to an eigenvalue problem.

Eigen

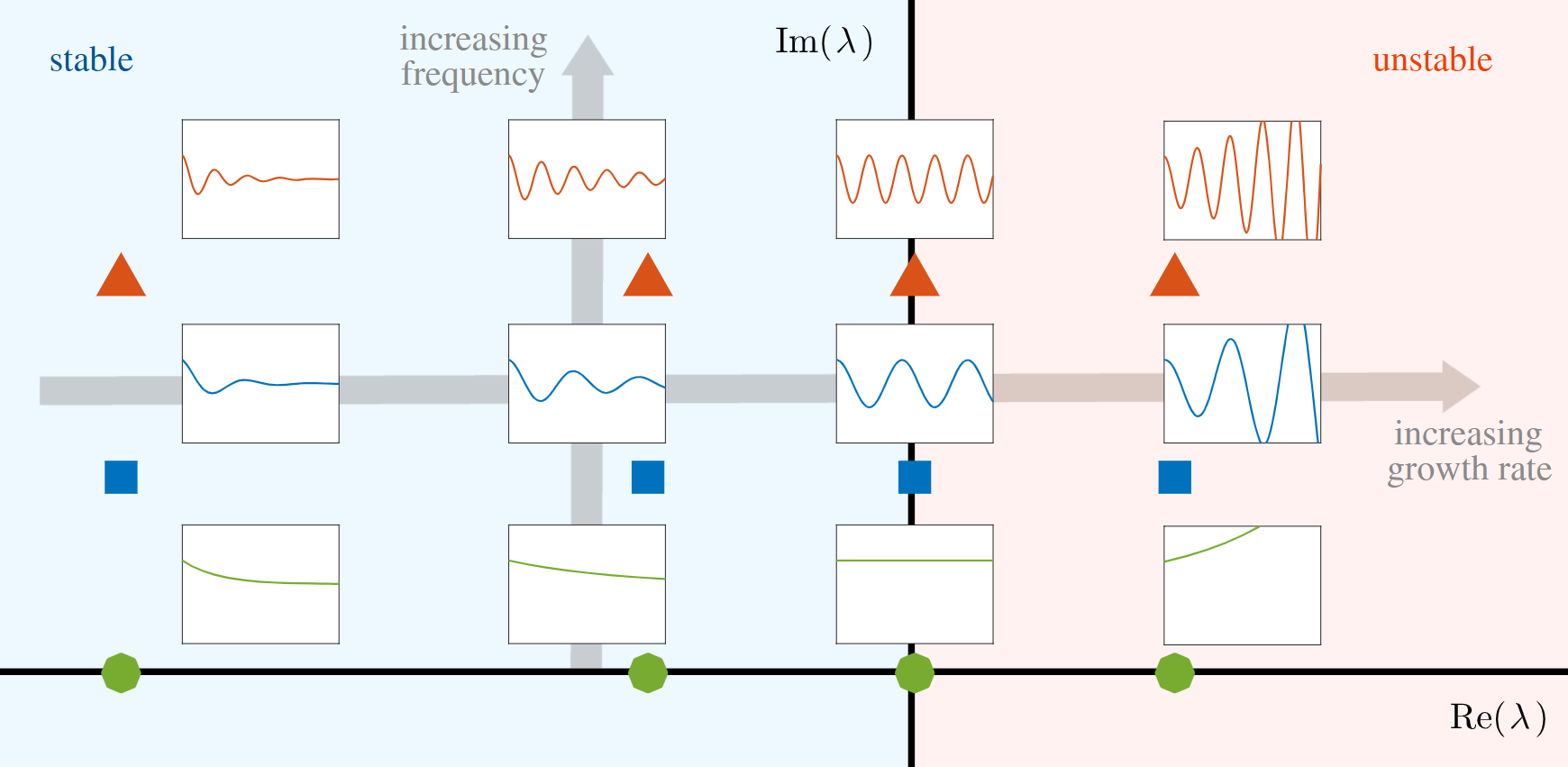
The eigenvalues and eigenvectors of a matrix (linear operator)capture the directions in which vectors can grow or shrink. Location in the eigenvalue spectrum determines whether a mode grows (unstable: \(Re(λ) > 0\)), decays (stable: \(Re(λ) < 0\)) or oscillates (complex frequency: \(Im(λ) \uparrow\))

LinearSystemEigenvalues

1Modal Analysis of Fluid Flows: An Overview. Kunihiko Taira, Steven L. Brunton, Scott T. M. Dawson, Clarence W. Rowley, Tim Colonius, Beverley J. McKeon, Oliver T. Schmidt, Stanislav Gordeyev, Vassilios Theofilis, and Lawrence S. Ukeiley. AIAA Journal 2017 55:12, 4013-4041

◀ ▶