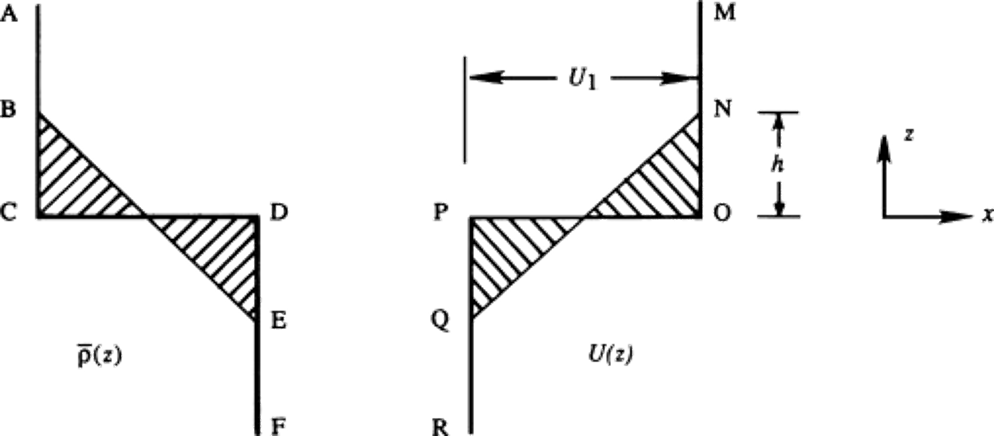
The energy source for the Kelvin-Helmholtz instability is the kinetic energy of the two streams.The disturbances evolve to smear out the gradients until they cannot grow further. Unstable waves at the interface transform the sharp density profile ACDF → ABEF and the velocity profile MOPR → MNQR
The high-density fluid in depth range DE is raised upward and mixed with the lower-density fluid in BC, so the potential energy of the system increases The required energy is drawn from the kinetic energy of the basic field, and the kinetic energy of MOPR is larger than that of MNQR
Assume lower-layer velocity is zero and upper-layer velocity is $U_1$ $$ U(z) = \frac{U_1}{2}\left(1 + \frac{z}{h}\right), \quad \bar{\rho}(z)=\rho_2 - \frac{\rho_2 - \rho_1}{2}\left(1 + \frac{z}{h}\right) \quad -h \leq z \leq h $$ Initial and final kinetic energies per unit width $$ E_{\text{initial}} = \frac{1}{2} \rho_1 U_1^2 h, \qquad E_{\text{final}} = \frac{1}{3} \rho_1 U_1^2 h + \frac{1}{12} (\rho_2 - \rho_1) U_1^2 h $$ Thus, when $(\rho_2 - \rho_1) \ll \rho_1$, kinetic energy decreases while total momentum $(=\int U dz)$ is nearly unchanged
◀ ▶