In the presence of the wall, then, the effect of friction is to break the constraint of exact geostrophic balance and produce a flow across the isobars from high to low pressure, which implies that work is being done on the fluid in the Ekman layer by the pressure force. This work by the pressure force supplies the necessary energy to maintain the Ekman layer
The rate $\dot{W}$, which represents the work done by the pressure force in the Ekman layer, is given by $$ \dot{W} = \int_0^\infty \left(-v \frac{\partial p}{\partial y}\right) dz = \frac{\rho U^2}{2} f \delta_E = \rho \, \frac{U^2}{2} \{2 A_v f\}^{1/2} $$ and represents the rate energy must be supplied to each unit area of the Ekman layer to maintain it
A geostrophic layer of fluid of depth $D$, moving with velocity $U$, has kinetic energy per unit area $ K = \rho \frac{U^2}{2} D $
If no external energy source is provided, the geostrophic flow decays through viscous dissipation. The decay time $\tau$ can be estimated as $$ \tau = \frac{K}{\dot{W}} = \frac{ \rho \tfrac{U^2}{2} D}{ \tfrac{\rho U^2}{2} (2 A_v f)^{1/2}} = \frac{D}{(2 A_v f)^{1/2}} $$ For geostrophic energy to decay slowly (long compared to a rotation period $f^{-1}$) $$ \tau f = \frac{D}{\delta_E} \gg 1, \delta_E = \left(\frac{2 A_v}{f}\right)^{1/2} \Rightarrow \tau f = \left( \frac{D^2 f}{2 A_v} \right)^{1/2} = E_v^{-1/2} $$ where $E_v$ is the Ekman number, $\tau$ measures the effectiveness of friction, as the “spin-down” time. Note that $\tau$ is independent of the relative velocity, and depends only on $f$ and $\delta_E$

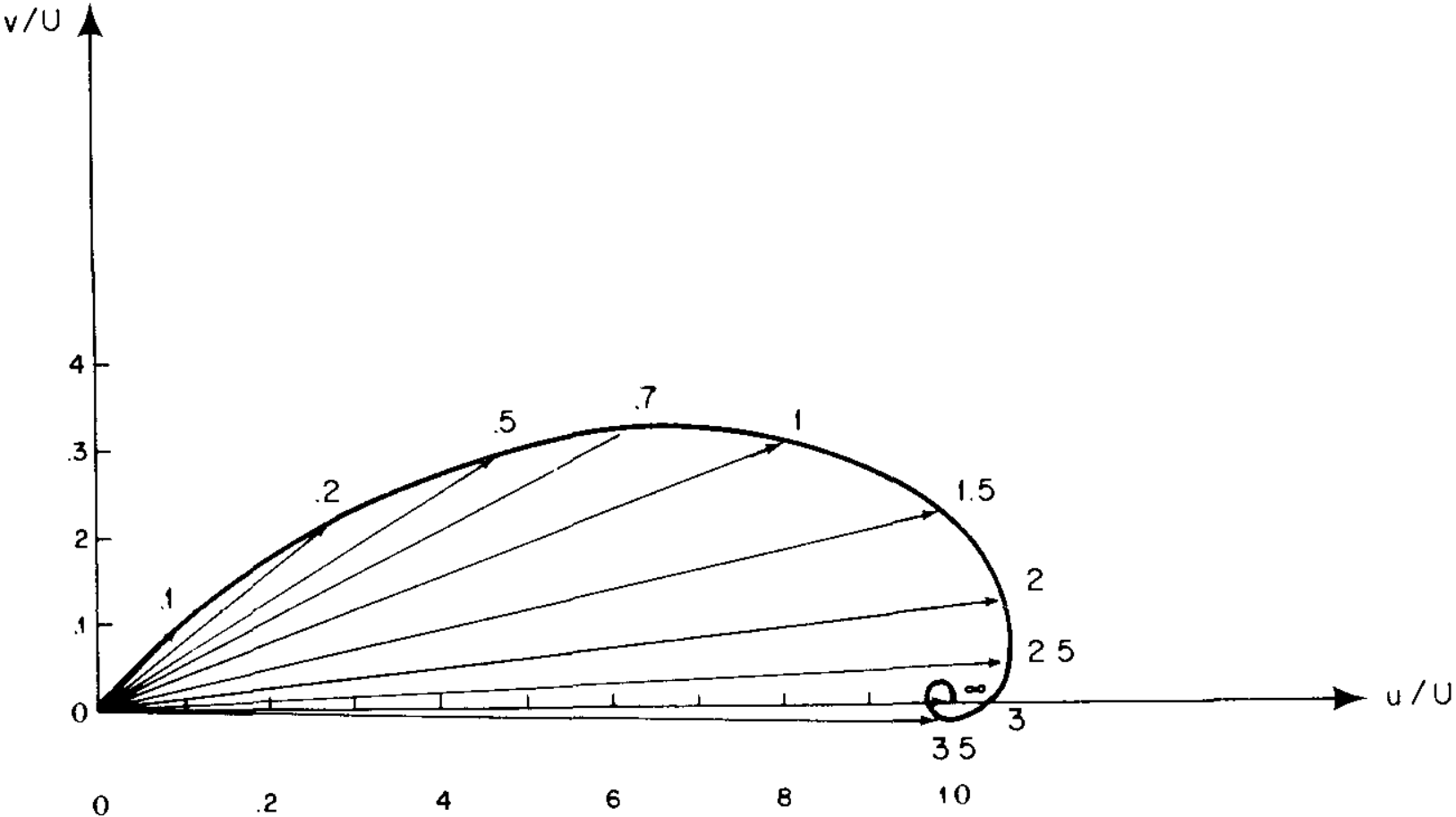
Another remarkable feature of the Ekman layer is the graceful turning of the velocity vector as the wall is approached. The velocity vector within the Ekman layer traces a spiral as depth decreases. Each layer is slowed by friction and rotated by the Coriolis force, causing a gradual turning of the vector. As the surface is approached, $$ \lim_{z \to 0} \frac{v}{u} = 1 $$ so that the velocity vector has turned $45^\circ$ to the left of the geostrophic velocity