The Ekman Layer

Define the horizontal vorticity components $$ \zeta = - \frac{\partial v}{\partial z}, \qquad \eta = + \frac{\partial u}{\partial z} $$ These describe how the horizontal flow varies with depth

Differentiate the $x$-momentum and $y$-momentum equation with respect to $z$ \[-f \frac{\partial v}{\partial z} = A_v \frac{d^3 u}{dz^3} \Rightarrow f\zeta = A_v \frac{d^2 \eta}{dz^2}\] \[f \frac{\partial u}{\partial z} = A_v \frac{d^3 v}{dz^3} \Rightarrow f\eta = A_v \frac{d^2 \zeta}{dz^2} \] $$ 0 = + f \frac{\partial v}{\partial z} + A_v \frac{\partial^2 \eta}{\partial z^2}, \qquad 0 = + f \frac{\partial u}{\partial z} + A_v \frac{\partial^2 \zeta}{\partial z^2} $$

The Ekman layer is established as a balance between the vorticity diffusion from the boundary and the compensating tilting of the planetary vorticity filaments.

The requirement that $u$ should decrease from $U$ to zero as the boundary is approached requires $\eta \neq 0$, and this in turn requires $v \neq 0$, so that the diffusion of $\eta$ can be balanced by the tilting of vortex filaments in the $y$-direction by $\partial v / \partial z$
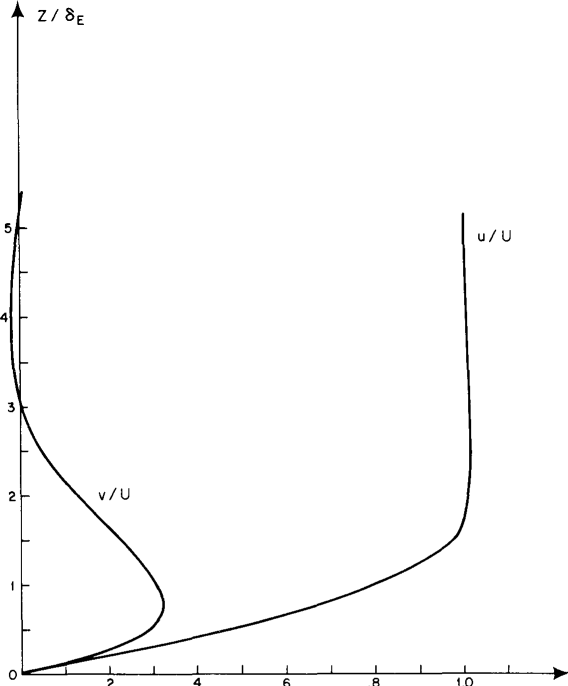
The figure shows the profiles of the velocity components $u$ and $v$. Far from the wall the velocity is entirely in the $x$-direction, which is the direction of the geostrophic flow. As the wall is approached, the retarding effect of friction decreases $u$. However, the pressure gradient in the $y$-direction is independent of $z$ and is therefore balanced only at infinity by the $y$-component of the Coriolis force. As $u$ decreases, this Coriolis force weakens, and in the presence of the pressure force in the $y$-direction, a velocity $v$ in that direction must be produced, flowing from high pressure to low pressure, retarded only by fluid friction

¹ Pedlosky, J. (1982). Geophysical Fluid Dynamics. Springer study edition. Springer, Berlin, Heidelberg.

◀ ▶