Discretization Approaches
Finite Difference Method
- The simplest numerical solution method
- Approximates derivatives at grid points
- Neglected lately, but has high potential for higher-order methods
Finite Volume Method
- The most widely used method (used in all major commercial codes and in OpenFOAM)
- Approximates integral equations, per construction conservative, simple up to second order
- Applicable to arbitrary polyhedral control volumes
- Difficult to extend to higher orders (many integration points)
Finite Element Method
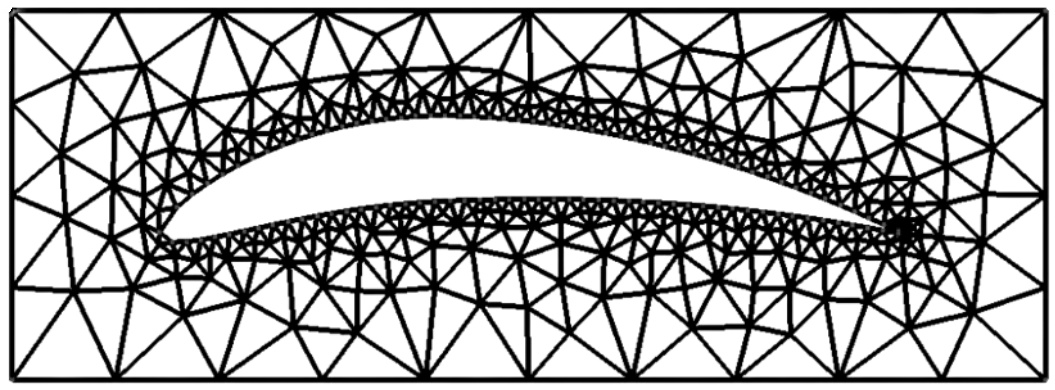
- Requires assembling sparse global matrices from element matrices, and most computation time spent in matrix assembly and iterative solvers for large-scale sparse systems
- Suitable for parallel computing
- Based on discretizing the domain into elements (triangles, tetrahedra, hexahedra, etc.) and nodes (vertices), and uses shape functions (interpolation functions) to approximate field variables within each element
- Finite-element solution doesn’t satisfy the differential equation(s), but satisfies a special weighted integral form
- Essential boundary conditions are satisfied exactly, and natural or gradient boundary conditions are satisfied approximately

1Course information of NFYK18001U High Performance Parallel Computing:
https://kurser.ku.dk/course/nfyk18001u