Finite Volume Approximation
The Finite Volume method is essentially a three-dimensional application of the finite difference method. It uses the the integral form of the conservation equations as its starting point. The solution domain is subdivided into a finite number of contiguous control volumes, and the conservation eqiatopms are applied to each control volume. At the centroid of each control volume lies a computational node at which the variable values are to be calculated
The Finite Volume method can accommodate any type of grid, so it is suitable for complex geometries. The grid defines only the control volume boundaries and need not be related to a coordinate system. The methid is conservative by construction, so long as surface integrals (which represent convection and diffusion fluxes) are the same for the control volumes sharing the boundary

The control volumes are of width $\Delta x$ and the boundaries (the dashed lines) are located half way between the nodes, at $x_{i \pm 1/2}$. If we approximate the integral by $\Delta x f_j$ and use the same one-sided approximation for the time derivative as we used for the finite difference approach, then the conservation law becomes $$ \frac{f_j^{n+1} - f_j^n}{\Delta t} = \frac{1}{\Delta x}(F_{\text{in}} - F_{\text{out}}) $$

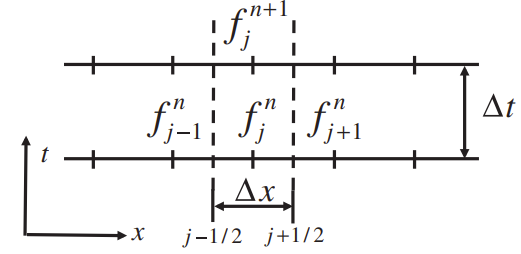
FiniteVolumeDiscretization

Evaluating the fluxes at the current time step and identifying $F_{\text{out}} = F_{j+1/2}^n$ and $F_{\text{in}} = F_{j-1/2}^n$ $$ \frac{f_j^{n+1} - f_j^n}{\Delta t} = \frac{F_{j+1/2}^n - F_{j-1/2}^n}{\Delta x} $$ To compute the fluxes, approximate $f$ at the $j+1/2$ boundary as the average of the average value of $f$ in the $j$ and the $j+1$ control volume and the first derivative of $f$ as the difference between $f_{j+1}$ and $f_j$, divided by $\Delta x$ $$ F_{j+1/2} = \frac{U}{2}(f_{j+1} + f_j) - D\left(\frac{f_{j+1} - f_j}{\Delta x}\right) $$

1Ferziger, Joel & Perić, Milovan & Street, Robert. (2020). Computational Methods for Fluid Dynamics. 10.1007/978-3-319-99693-6.

◀ ▶