Finite Difference
Local truncation error of central difference
\begin{align}
\epsilon &= \frac{\delta^{+}(h_n) + \delta^{-}(h_n)}{2}
- \left.\frac{\partial h}{\partial x}\right|_{x = x_n}
= \frac{h_{n+1} - h_{n-1}}{2\Delta x}
- \left.\frac{\partial h}{\partial x}\right|_{x = x_n} \\[6pt]
&= \frac{h_n + \Delta x h' + \tfrac{\Delta x^2}{2} h''
- \Big(h_n - \Delta x h' + \tfrac{\Delta x^2}{2} h''\Big)
+ \mathcal{O}(\Delta x^3)}{2\Delta x} - h' \\[6pt]
&= \mathcal{O}(\Delta x^2)
\end{align}
with $h' = \left.\frac{\partial h}{\partial x}\right|_{x_n}, \quad h'' = \left.\frac{\partial^2 h}{\partial x^2}\right|_{x_n}, \ldots$
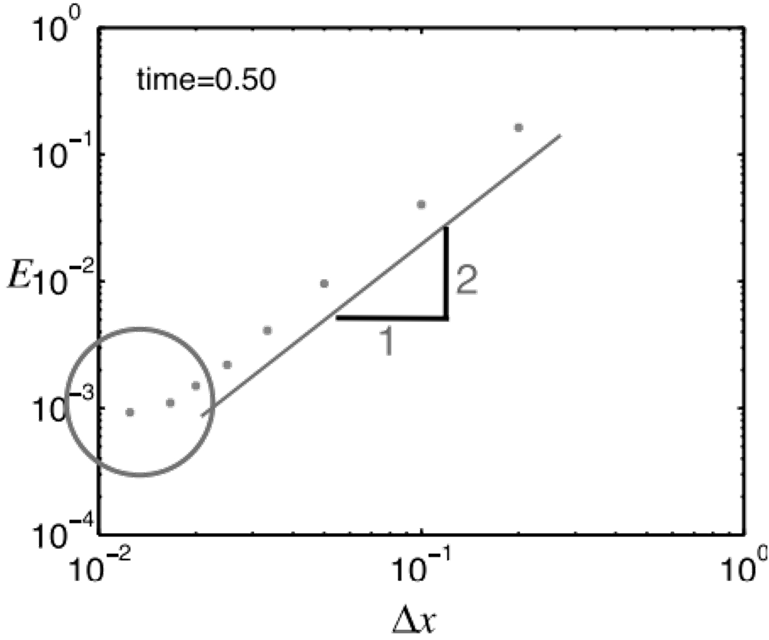
Truncation error $\epsilon$ is second order in $\Delta x$, and therefore much better than forward difference
Numerical schemes where the original differential operator goes to zero are
generally called consistent. Although almost all schemes used in practice are consistent, sometimes minor modifications lead to inconsistent schemes
Approximate differential equation with finite differences, e.g.
$$
\frac{\partial h}{\partial t} = -c^2 \frac{\partial u}{\partial x}
\;\;\;\;\rightarrow\;\;\;\;
\frac{\partial h}{\partial t} = -c^2 \, \delta^{-}(u_n)
$$
Boundary conditions are set by 'ghost' points $x_0$ and $x_{N+1}$.
Kinematic boundary condition (no flow normal to boundary)
$$
u(x_0) = 0 , \quad u(x_{N+1}) = 0
$$
Periodic boundary conditions
$$
u(x_0) = u(x_N), \quad u(x_{N+1}) = u(x_1)
$$
◀
▶