Kelvin Wave
\[
\begin{aligned}
&\underbrace{\frac{\partial \eta}{\partial t} + H \frac{\partial u}{\partial x}
\quad \xrightarrow[\text{Assume } \eta = \hat{\eta}(y) e^{i(kx - \omega t)}]{\partial_t \to -i\omega,\; \partial_x \to ik} \quad
-i\omega \hat{\eta} + ikH \hat{u} = 0}_{\text{Contributes to dispersion relation between } \omega \text{ and } k} \\[1.5ex]
&\underbrace{\frac{\partial u}{\partial t} = -g \frac{\partial \eta}{\partial x}
\quad \xrightarrow[\text{Assume } u = \hat{u}(y) e^{i(kx - \omega t)}]{\partial_t \to -i\omega,\; \partial_x \to ik} \quad
-i\omega \hat{u} = -ikg \hat{\eta}}_{\text{Contributes to dispersion relation between } \omega \text{ and } k} \\[1.5ex]
&\underbrace{fu = -g \frac{\partial \eta}{\partial y}
\quad \xrightarrow[\text{Use } u, \eta = \hat{u}(y), \hat{\eta}(y) e^{i(kx - \omega t)}]{\partial_y \text{ acts only on } \hat{\eta}(y)} \quad
f \hat{u} = -g \frac{d\hat{\eta}}{dy}}_{\text{Determines transverse dependence}}
\end{aligned}
\]
\(
\begin{aligned}
&\hat{u} = \frac{-ikg \hat{\eta}}{-i\omega}
= \frac{\cancel{-} \cancel{i} k g \hat{\eta}}{\cancel{-} \cancel{i} \omega}
= \frac{k g \hat{\eta}}{\omega}
\quad \text{(from } -i\omega \hat{u} = -ikg \hat{\eta} \text{)} \\
&-i\omega \hat{\eta} + ikH \hat{u} = 0
\quad \Rightarrow \quad
-i\omega \hat{\eta} + ikH \cdot \frac{k g \hat{\eta}}{\omega} = 0
\quad \Rightarrow \quad
\hat{\eta} (\omega^2 - gHk^2) = 0
\end{aligned}
\)
A non-trivial solution is therefore possible only if
\(\boxed{
\omega = \pm k \sqrt{gH}}
\)
so that the wave propagates with a non-dispersive speed
$$
c = \sqrt{gH}
$$
The propagation speed of a Kelvin wave is therefore identical to that of non-rotating gravity waves.
Its dispersion equation is a straight line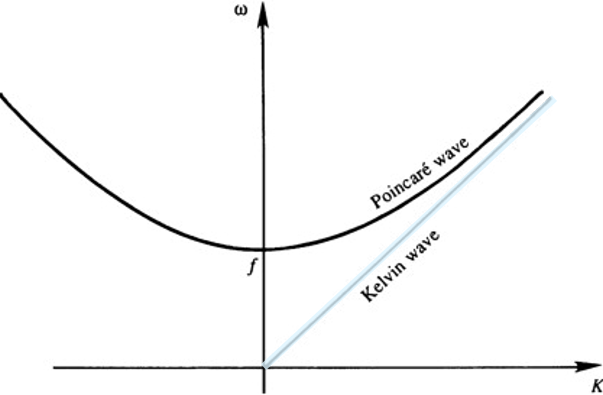 All frequencies are possible.
All frequencies are possible.
◀
▶
 All frequencies are possible.
All frequencies are possible.