Dispersion Relation for Rossby Waves
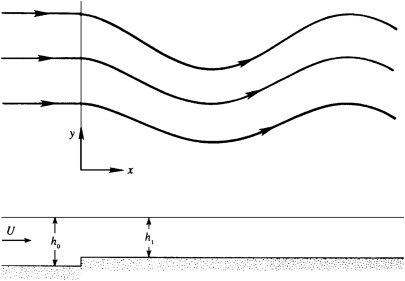
Frequently, Rossby waves are superposed on a strong eastward mean current, such as the atmospheric jet stream. If $U$ is the speed of this eastward current, then the observed eastward phase speed is $$ c_x = U - \frac{\beta}{k^2 + l^2 + f_0^2 / c^2} $$ Stationary Rossby waves can therefore form when the eastward current cancels the westward phase speed, giving $c_x = 0$

This is how stationary waves are formed downstream of the topographic step in EastwardVorticity

$$ c_x = U - \frac{\beta}{\,k^2 + \underbrace{l^2}_{\text{assume } l = 0} + \underbrace{\cancel{\dfrac{f_0^2}{c^2}}}_{\text{negligible for barotropic flow}}} \ \rightarrow\ \underbrace{U = \frac{\beta}{k^2}}_{\substack{\text{stationary Rossby waves,}\\\text{the eastward current cancels}\\\text{the westward phase speed,} \\c_x = 0}}\ \rightarrow\ \underbrace{\lambda = 2\pi\left(\frac{U}{\beta}\right)^{1/2}}_{\text{wavelength}} $$ ◀ ▶