The phase speed reaches a maximum when $k^2 + l^2 \to 0$, corresponding to very large wavelengths represented by the region near the origin of 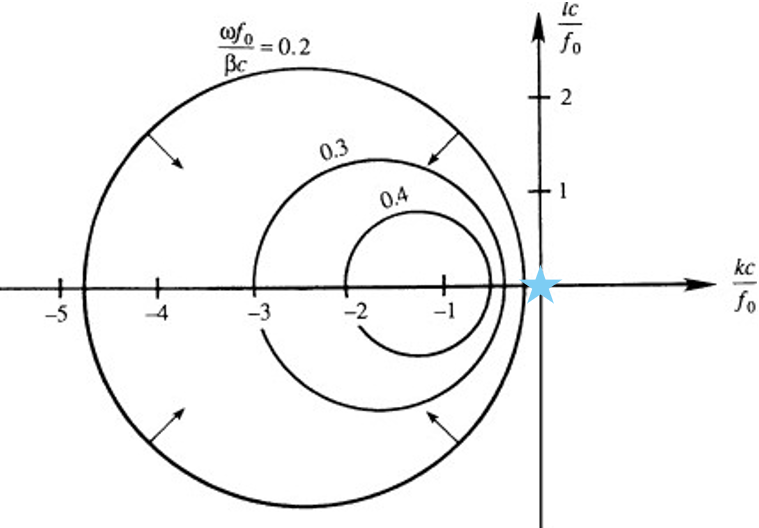. In this region the waves are nearly non-dispersive and have an eastward phase speed $c_x \cong -\beta c^2 / f_0^2$. With $\beta = 2 \times 10^{-11}\ \text{m}^{-1} \text{s}^{-1}$, a typical baroclinic value of $c \sim 2\ \text{m/s}$, and a mid-latitude value of $f_0 \sim 10^{-4}\ \text{s}^{-1}$, this gives $c_x \sim 10^{-2}\ \text{m/s}$. At these slow speeds the Rossby waves would take years to cross the width of the ocean at mid-latitudes. Rossby waves in the ocean are therefore more important at lower latitudes, where they propagate faster.
However, the dispersion relation \(\boxed{\omega = -\frac{\beta k}{k^2 + l^2 + f_0^2/c^2}}\) is not valid within a latitude band of $3^\circ$ from the equator for which the assumption of a near geostrophic balance breaks down.
In the atmosphere $c$ is much larger, and consequently the Rossby waves propagate faster. A typical large atmospheric disturbance can propagate as a Rossby wave at a speed of several meters per second.