\[\boxed{\omega = -\frac{\beta k}{k^2 + l^2 + f_0^2/c^2}}\] $\omega(k,l)$ can be displayed as a surface, taking $k$ and $l$ along Cartesian axes and plotting contours of constant $\omega$
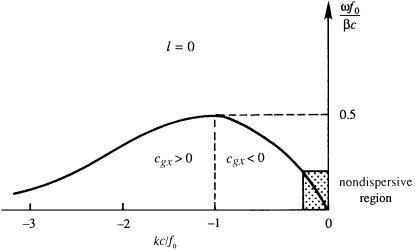
Dispersion relation $\omega(k,l)$ for a Rossby wave with $\omega$ versus $k$ for $l = 0$. Regions of positive and negative group velocity $c_{gx}$ are indicated.
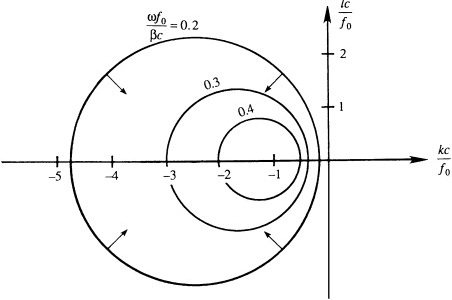
A plane view of the surface $\omega(k,l)$, showing contours of constant $\omega$ on a $kl$-plane. Arrows perpendicular to the largest circular constant-$\omega$ contour indicate directions of the group velocity vector $\mathbf{c_g}$. These contours are circles because \(\boxed{\omega = -\frac{\beta k}{k^2 + l^2 + f_0^2/c^2}}\) can be written as \[ \left(k + \frac{\beta}{2\omega}\right)^2 + l^2 = \left(\frac{\beta}{2\omega}\right)^2 - \frac{f_0^2}{c^2} \]