Quasi-Geostrophic Vorticity Equation
To derive the governing equation for quasi-geostrophic motions using the customary β-plane approximation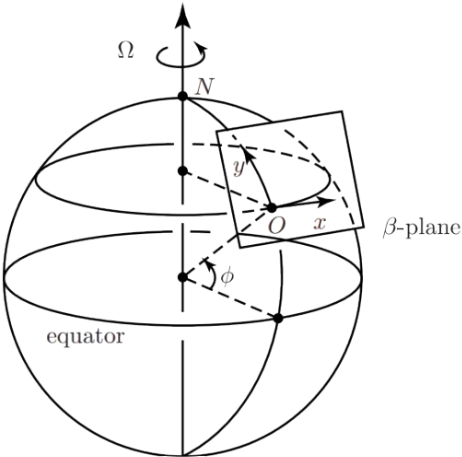 
valid for $\beta y \ll f_0$,
the first step is to simplify the vorticity equation for quasi-geostrophic motions,
assuming that the velocity is geostrophic to the lowest order.
The small departures from geostrophy are important because they determine the evolution of the flow with time
valid for $\beta y \ll f_0$,
the first step is to simplify the vorticity equation for quasi-geostrophic motions,
assuming that the velocity is geostrophic to the lowest order.
The small departures from geostrophy are important because they determine the evolution of the flow with time
Start with the shallow-water potential vorticity equation
$$
\frac{D}{Dt}
\left(
\underbrace{\frac{\zeta + \overbrace{f}^{\text{$f = f_0 + \beta y$}}}{h}}_{\text{potential vorticity in shallow-water}}
\right) = 0
$$
$$
\begin{aligned}
\frac{D}{Dt}\!\left(\frac{\zeta+f}{h}\right)=0
&\;\mathrel{\underset{\text{write as product with }h^{-1}}{\Rightarrow}}\;
\frac{D}{Dt}\!\left[(\zeta+f)h^{-1}\right]=0 \\[6pt]
&\;\mathrel{\underset{\text{product rule}}{\Rightarrow}}\;
h^{-1}\frac{D}{Dt}(\zeta+f)+(\zeta+f)\frac{D}{Dt}(h^{-1})=0 \\[6pt]
&\;\mathrel{\underset{\text{chain rule on }h^{-1}}{\Rightarrow}}\;
\frac{D}{Dt}(h^{-1})=-h^{-2}\frac{Dh}{Dt} \\[6pt]
&\;\mathrel{\underset{\text{substitute}}{\Rightarrow}}\;
h^{-1}\frac{D}{Dt}(\zeta+f)-(\zeta+f)h^{-2}\frac{Dh}{Dt}=0 \\[6pt]
&\;\mathrel{\underset{\text{multiply by }h^{2}}{\Rightarrow}}\;
h\,\frac{D}{Dt}(\zeta+f)-(\zeta+f)\frac{Dh}{Dt}=0
\end{aligned}
$$
◀
▶