Kelvin Wave
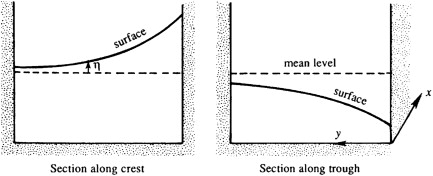
TwoTransverseSectionsWave

Free-surface distribution in a Kelvin gravity wave propagating into the plane of the paper (the x-direction) within a channel aligned with x-direction. The wave crests and troughs are enhanced on the right side of the channel.

Two transverse sections of the wave, one through a crest (left panel) and the other through a trough (right panel). The wave is propagating into the plane of the paper so that the fluid velocity under the crest is into the plane of the paper and that under the trough is out of the plane of the paper. The constraints of the sidewalls require that \( v = 0 \) at the walls, and we are exploring the possibility of a wave motion in which \( v \) is zero everywhere.
The linearized momentum equation along the y-direction: \[ \frac{\partial v}{\partial t} + f u = -g \frac{\partial \eta}{\partial y} \] requires that \( fu \) can only be geostrophically balanced by a transverse slope of the sea surface across the channel: \[ fu = -g \frac{\partial \eta}{\partial y} \]

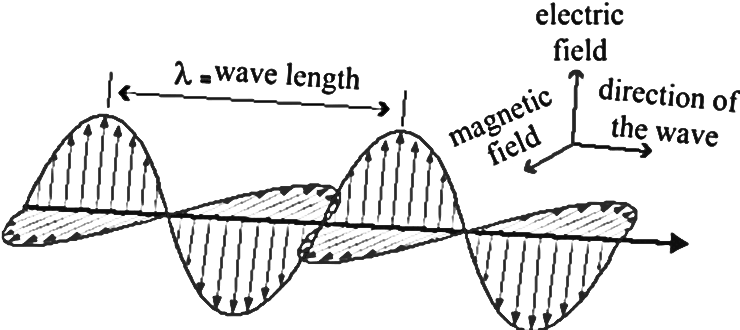
1Transverse waves are characterised by the fact that the displacement caused by them is perpendicular to the direction of their movement TransverseWave.

◀ ▶