Kelvin Wave
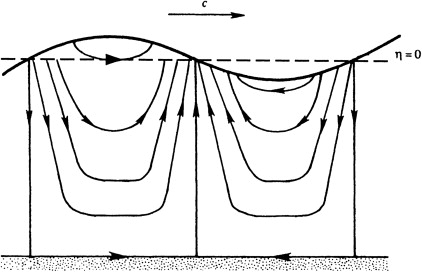
Instantaneous streamline pattern for a sinusoidal surface wave propagating to the right. Here, the $\psi = 0$ streamline follows the bottom and jumps up to contact the surface where $\eta = 0$.
The remaining streamlines start and end on the liquid surface with purely horizontal motion found in the $+x$ direction below a wave crest and in $-x$ direction below a wave trough.